Information theory is a subject with very rich intellectual contents, and it is somewhat philosophical. Information theory was founded by Bell Telephone Laboratory scientist Claude Shannon, with the seminal paper “The Mathematical Theory of Communication” in 1948. Information theory studies fundamental limits in communications, in the form of transmission, storage, etc.
There are two key concepts in information theory:
- Information is uncertainty, and so an information source is modeled as a random variable.
- Information is digital, transmission should be 0’s and 1’s with no reference to what they represent.
Fundamental Theorems
The first theorem is the source coding theorem that establishes the fundamental limit in data compression. The idea of the source coding theorem is that no matter how smart the data compression algorithm is designed, there is always a minimum size that the file can be compressed.
The second theorem is the channel coding theorem that establishes the fundamental limit for reliable communication through a noisy channel. The idea is that no matter how smart the communication (system) is designed, for reliable communication, there exists a maximum rate that information can be transmitted through the channel. This quantity is called the channel capacity.
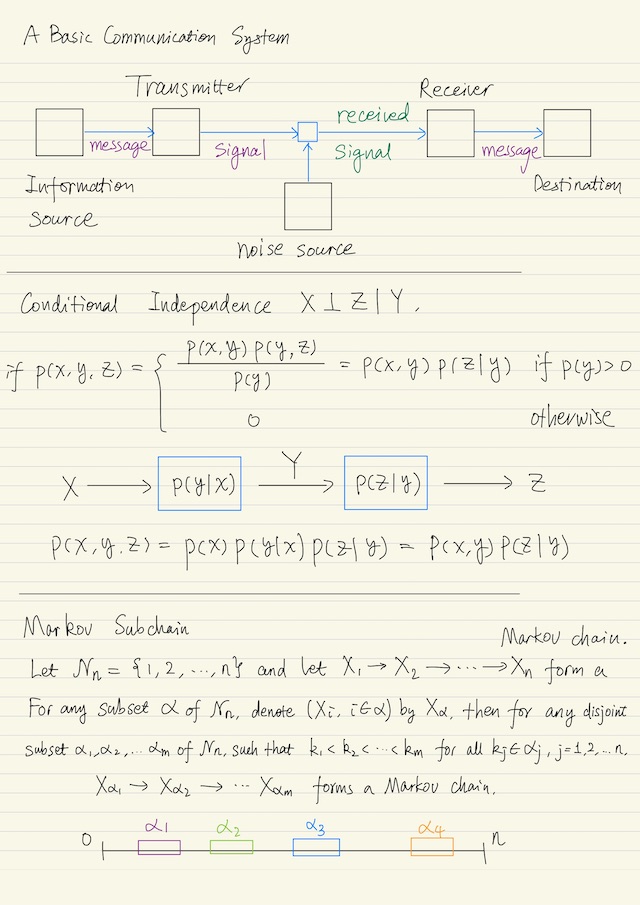
Independence and Markov Chain
X denotes a discrete random variable taking values in a set ? (script X, called the alphabet of the random variable X). Then:
{pX(x)}is the probability distribution for random variable X.SXis the support of X, i.e.,{x ∈ ? | pX(x) > 0}. If SX = ?, we say that p is strictly positive. Non-strictly positive distributions are dangerous, we need to handle them with great care.
Recall some basic definitions:
Independence. Two random variables X and Y are independent, denoted by X ⊥ Y, if p(x, y) = p(x) p(y) for all x and y, i.e.for all (x, y) ∈ ? × ?.
Mutual independence. When n ≥ 3, random variable X1, X2, … Xn are mutually independent if for all x1, x2, … xn:
p(x1, x2, ..., xn) = p(x1) p(x2) ... p(xn)Pairwise Independence. Pairwise Independence is implied by mutual independence but not vice versa. When n ≥ 3, random variable X1, X2, … Xn are pairwise independent if Xi and Xj are independent for all 1 ≤ i < j ≤ n.
Conditional Independence. For random variable X, Y, and Z; X is independent of Z conditioning on Y, denoted by X ⊥ Z | Y, if:
if p(y) > 0:
p(x, y, z) = p(x, y) p(y, z) / p(y) = p(x, y) p(z | y)
otherwise:
p(x, y, z) = 0Proposition: For random variables X, Y, and Z. X ⊥ Z | Y if and only if p(x, y, z) = a(x, y) b(y, z), for all x, y, and z such that p(y) > 0. Here a(x,y) and b(y,z) are not necessarily probability distributions: a is a function that depends only on x and y, and b is a function that depends only on y and z. Note however, that the choice of a(x,y) and b(y,z) is not unique.
Markov Chain. For random variables X1, X2, …, Xn, where n ≥ 3, X1 → X2 → … → Xn forms a Markov chain if:
if p(x2), p(x3), ... p(xn-1) > 0:
p(x1, x2, ..., xn) = p(x1, x2) p(x3 | x2) ... p(xn | xn-1)
otherwise:
p(x1, x2, ..., xn) = 0X1 → X2 → X3 is equivalent to X1 ⊥ X3 | X2.
Proposition: X1 → X2 → … → Xn forms a Markov chain if and only if Xn → Xn-1 → … → X1 forms a Markov chain.
Proposition: X1 → X2 → … → Xn forms a Markov chain if and only if
- X1 → X2 → X3
- (X1, X2) → X3 → X4
- …
- (X1, X2, …, Xn-2) → Xn-1 → Xn
form a Markov chain.
Proposition: X1 → X2 → … → Xn forms a Markov chain if and only if
p(x1, x2, ..., xn) = f1(x1, x2) f2(x2, x3) ... fn-1(xn-1, xn)for all x1, x2, …, xn such that p(x2), p(x3), …, p(xn-1) > 0.
Proposition: Markov Subchain. Let ?n be the index set = {1, 2, …, n} and let X1 → X2 → … → Xn form a Markov chain. For any subset ɑ of ?n, denote (Xi, i ∈ ɑ) by Xɑ. Then for any disjoint subsets ɑ1, ɑ2, …, ɑm of ?n such that k1 < k2 < … < km for all kj ∈ ɑj, j = 1, 2, …, m, we have Xɑ1 → Xɑ2 → … → Xɑm forms a Markov chain. That is a subchain of a Markov chain is also a Markov chain.
Shannon’s Information Measures
There are 4 types of Shannon’s information measures:
- Entropy
- Conditional entropy
- Mutual information
- Conditional mutual information
Entropy
Entropy measures the uncertainty of a discrete random variable. The entropy H(X) of a random variable X is defined as Hɑ(X) = -Σx p(x) logɑ p(x). The convention is the summation is taken over the support of X, i.e SX. The entropy of a random variable is positive.
The unit of entropy is:
| bit (different from a bit in computer science) | if ɑ = 2 |
| nat | if ɑ = e |
| D-it | if ɑ = some positive integer D |
H(X) depends only on the distribution of X but not on the actual values taken by X, hence also written as H(pX).
Entropy can also be expressed as expectation. The expectation of g(X) for some random variable X is
E[g(X)] = Σx p(x) g(x)where the summation is over the support of X. We also have linearity for expectation, so E[ f(X) + g(X) ] = E[f(X)] + E[g(X)]. So we can write entropy of X as below:
H(X) = -E[log p(X)] = -Σx p(x) log p(x)Note: in probability theory, when expectation of g(x) for random variable is considered, usually g(x) depends only on the value of x but not on the probability of x. In information theory, this is not the case.
Binary Entropy Function
For 0 ≤ γ ≤ 1, define the binary entropy function hb(γ) = -γ log(γ) -(1 - γ) log(1 - γ) with the convention that 0 log0 = 0, as by L’Hopital’s rule lima→0 a log(a) = 0.
For binary variable X with distribution γ and 1 – γ, H(X) = hb(γ). hb(γ) achieves the maximum value 1 when γ = 1/2.
Joint Entropy
The joint entropy H(X, Y) of a pair of random variables X and Y is defined as:
H(X, Y) = -Σx,y p(x, y) log p(x, y) = -E log p(X, Y)Conditional Entropy
For random variables X and Y, the conditional entropy of Y given X is defined as:
H(Y|X) = -Σx,y p(x,y) log p(y|x) = -E log p(Y|X)Note when we cover up the conditioning of X, this reduces to the usual definition for the entropy of Y.
The conditional entropy of Y given X is equal to the way the sum of the conditional entropy of Y given a particular x over the distribution p(x).
H(Y|X) = Σx p(x) H(Y|X=x)Similarly, we can write H(Y|X,Z) = Σz p(z) H(Y|X, Z = z), where
H(Y|X, Z=z) = -Σx,y p(x,y|z) log p(y|x,z)Note that when we cover up the conditioning on a particular z, this formula reduces to the usual definition of entropy of Y given X.
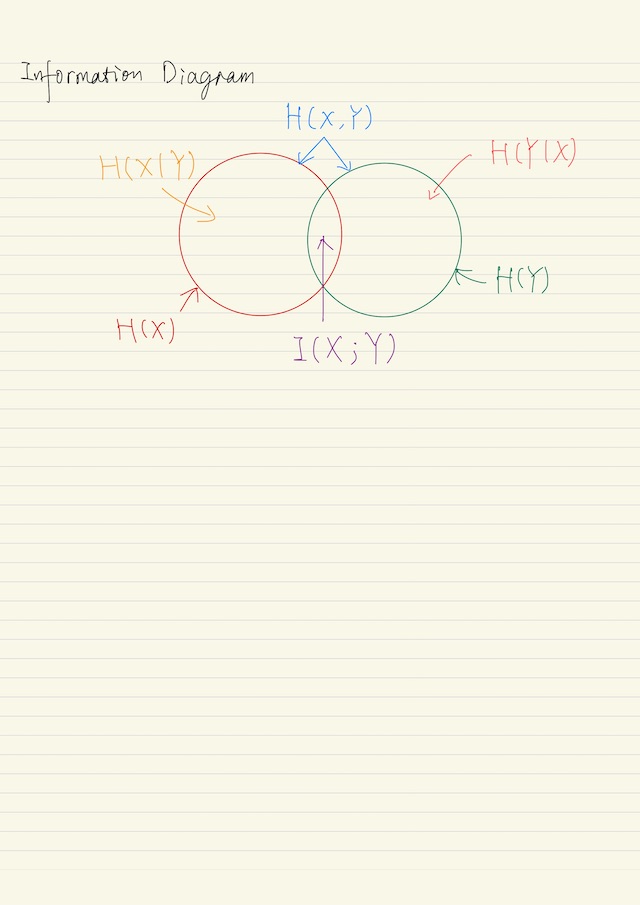
Proposition. H(X,Y) denotes the uncertainty contained in the random variables X and Y.
H(X, Y) = H(X) + H(Y|X) = H(Y) + H(X|Y)On the left hand side, consider that X and Y are revealed in “one step”. On the right hand side imagine that we reveal X and Y in “two steps”. Either way, the total amount of entropy is actually the same.
Mutual Information
For random variables X and Y, the mutual information between X and Y is defined as:
I(X;Y) = Σx,y p(x,y) log( p(x,y)/[p(x)p(y)] )
= E log( p(X,Y)/[p(X)p(Y)] )I(X;Y) is symmetrical in X and Y. Alternatively, it can be written as:
I(X;Y) = Σx,y p(x,y) log( p(x,y)/[p(x)p(y)] )
= Σx,y p(x,y) log( p(x|y)/p(x) )
= E log( p(X|Y)/p(X) )Proposition. The mutual information between a random variable X and itself is equal to the entropy of X:
I(X;X) = H(X)The entropy of X is sometimes called the self-information of X.
Proposition. The mutual information between X and Y is equal to the amount of information that we can obtain about X by knowing Y.
I(X;Y) = H(X) - H(X|Y)
I(X;Y) = H(Y) - H(Y|X)
⟹ I(X;Y) = H(Y) - H(Y|X)
⟹ I(X;Y) = H(Y) - ( H(X, Y) - H(X) )
⟹ I(X;Y) = H(Y) + H(X) - H(X, Y)The last equation is analogous to the set theoretical equation μ(A∩B) = μ(A) + μ(B) - μ(A∪B), where μ is a set additive function and A and B are sets.
Conditional Mutual Information
For random variables X, Y and Z, the mutual information between X and Y conditioning on Z is defined as
I(X;Y|Z) = Σx,y,z p(x,y,z) log( p(x,y|z) / [ p(x|z) p(y|z) ] )
= E log( p(X,Y|Z) / [ p(X|Z) p(Y|Z) ] )I(X;Y|Z) is symmetrical in X and Y. Similar to entropy we have I(X;Y|Z) = Σz p(z) I(X;Y | Z=z), where
I(X;Y | Z=z) = Σx,y p(x,y|z) log( p(x,y|z) / [p(x|z) p(y|z)] )Proposition. The mutual information between a random variable X and itself conditioning on a random variable Z is equal to the conditional entropy of X given Z, i.e. I(X;X | Z) = H(X | Z).
Proposition.
I(X;Y | Z) = H(X | Z) - H(X | Y,Z)
I(X;Y | Z) = H(Y | Z) - H(Y | X,Z)
I(X;Y | Z) = H(Y | Z) + H(X | Z) - H(X, Y |Z)For more on Shannon’s Information Measures, please refer to the wonderful course here https://www.coursera.org/learn/information-theory
Related Quick Recap
I am Kesler Zhu, thank you for visiting my website. Check out more course reviews at https://KZHU.ai
Don't forget to sign up newsletter, don't miss any chance to learn.
Or share what you've learned with friends!
Tweet