Public Key Encryption - KZHU.ai 🚀

Table of Contents

A public-key encryption scheme is composed of three probabilistic polynomial time algorithms:

Gen	The key-generation algorithm that on input 1ⁿ (where n is security parameter), outputs public key pk, and private key sk.
Enc	Encryption algorithm that on input pk and a message m, outputs a cipher text c.
Dec	Decryption algorithm that on input sk and a cipher text c, outputs a message m or an error ⊥.

Certainly, for all m and pk, sk output by Gen, if you decrypt using the private key something that was encrypted using the public key, you should get back the same results in the end, i.e. Dec_sk(Enc_pk(m)) = m.

CPA Security

CPA (Chosen Plaintext Attacks) security for public key encryption scheme can be defined in a way that’s very analogous to that in the private key settings. Fix a public key encryption scheme Π and an adversary A, then we can define the following experiment:

Run Gen(1ⁿ) to get keys pk, sk.
Give pk to A, who outputs (m₀, m₁) of same length.
Choose uniform b ∈ {0,1} and compute the cipher text c ← Enc_pk(m_b).
Give c to A.
A outputs a guess b’, and the experiment evaluates to 1 if b’ = b.

The public key encryption scheme Π is CPA-secure if for all probabilistic polynomial time adversary A, such that:

Pr[ PubKeyCPA_Π,A(n) = 1 ] ≤ 1/2 + negligible(n)

Note there is no encryption oracle, which is redundant in public key setting. This fact has a number of consequences:

There is no perfectly secret public key encryption, at least not in any of a setting where the attacker is able to get a copy of the recipient’s public key. This follows from the fact that, given the public key, the attacker effectively has access to an encryption oracle. Which means:
- Given any cipher text corresponding some unknown messages, the attacker could always try to encrypt every possible message under the public key repeatedly until it obtain the same cipher text.
- Alternatively, the attacker could also run the key generation algorithm over and over again, until it obtains a private key matching the observed public key.
No public key encryption scheme with a deterministic encryption algorithm can possibly be CPA-secure. This is exactly like what is in the setting of private key encryption. We should never use a deterministic public key encryption.
CPA-security implies security for encrypting multiple messages as in the private key case.

CCA Security

We could also consider the notion of CCA (Chosen Ciphertext Attacks) in the public key setting. The attacker might then:

Be able to inject cipher text c’.
Send the cipher text c’ to the recipient.
Receive in return the resulting decryption m’, corresponding to c’.

Chosen Ciphertext Attacks are arguably even a greater concern in the public setting than in the private setting.

Private key setting	The recipient shares the key with one other sender. The recipient will assume the messages come from the legitimate sender.
Public key setting	Anybody in the world, who is able to obtain a copy of public key, is a legitimate sender with respect to that receiver.

So, in the case of public key setting, it would be much easier for an attacker to:

Send a cipher text that would not immediately get rejected by the recipient.
Potentially receive in return the entire decryption m’ of the cipher text c’ that it sends to the receiver.

The point of all of this is that if you thought that Chosen Ciphertext Attacks were a problem in private key setting (and indeed they are), well they’re even more a concern in the public key setting.

Malleability

Informally, malleability refers to the property that, given a cipher text c (the encryption of some unknown message m), it is possible for an attacker to produce another cipher text c’, the decrypts to a related message m’. The malleability issue is even more problematic in the public key setting than it is in the private key setting.

Malleability and CCA security are very related. In particular any scheme which malleable will not be CCA secure. And conversely, a scheme that is secure against CCA will not be malleable.

Hybrid Encryption

Let us imagine we want to use a public key encryption scheme to encrypted a very long message m. One option is to simply use the encryption algorithm with public key pk and message m as input to obtain cipher text c. However public key encryption is relatively inefficient compared to private key encryption. We have another option by combining private key encryption and public key encryption to improve the efficiency.

The encryption is like this:

Select a random key k for some private key encryption scheme.
Encrypt the key k using the public key scheme with public key pk, to get “encapsulated key”.
Encrypt the message m using the private key scheme with key k, to get “cipher text”.

The decryption can be done in the obvious way. What the recipient can do, is to:

Use private key sk to decrypt the “encapsulated key” to get the key k.
Use the decryption algorithm for the private key encryption scheme with key k to recover message m from the “cipher text”.

So here we have something gives us the functionality of public key encryption, but asymptotically the efficiency here is the private key encryption scheme.

Security

Let Π be the public key component, and Π’ be the private key component, and Π_hy denote the combination. If Π is a CPA-secure public key scheme, Π’ is a CPA-secure private key scheme, then Π_hy is a CPA-secure public key scheme.

Similarly for CCA-security.

The hybrid encryption approach is one that is used all the time in practice and you never want to use a public key encryption natively to encrypt large volumes of data.

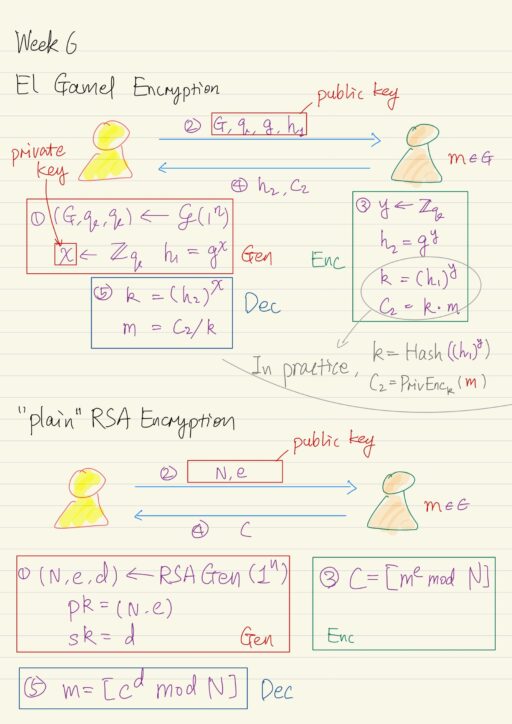
Discrete-Logarithm Based Encryption: El Gamal

Recall the Diffie-Hellman key exchange, we could do something more interesting with it. After one party derived the h₂, and key k (recall that h₂ = g^y and k = h₁^y), that party can use the key k to encrypt a message m (assuming that m ∈ G, where G is the group) securely. This encryption of m can be done simply by k × m, to get the cipher text c₂. The k is a uniform group element, c₂ will also be a uniform group element, and therefore contains no information about m. This form of encryption using k is indeed secure, as long as you use k in this way only once.

At the other end, the initial party can also compute the key k using h₂ just received, and their secret exponent x (recall that k = h₂^x). They can recover the message m by m = c₂ / k. At this point, we just have an encryption scheme, called El Gamal encryption scheme.

Gen(1ⁿ)	Run ?(1ⁿ) to obtain G, q, g. Choose uniform x ∈ Z_q. The public key is (G, q, g, h₁ = g^x). The private key is x.
Enc_pk(m) pk = (G, q, g, h₁), m ∈ G	Choose uniform y ∈ Z_q. The cipher text is h₂ = g^y and c₂ = h₁ × m = g^x × m.
Dec_sk(k, c₂) k = h₂^x	Output c₂ / k = c₂ / h₂^x.

An example: suppose G is the subgroup of Z^*₁₁ generated by g = 4, and order q = 5:

4¹ = 4 mod 11
4² = 16 = 5 mod 11
4³ = 64 = 9 mod 11
4⁴ = 256 = 3 mod 11
4⁵ = 1024 = 1 mod 11
4⁶ = 4096 = 4 mod 11 <-- begin to repeat
4⁷ = 16384 = 5 mod 11

From the calculation above G = {1, 3, 4, 5, 9}. Now suppose h₁ = 3, then x = 4:

privite key:
x = 4
public key:
G = {1, 3, 4, 5, 9}
g = 4
q = 5
h₁ = 3

On the other end, suppose y = 3, message we want to encrypt is m = 5, what is the encryption of the message? It shall be h₂ and c₂, i.e. (9, 3).

h₂ = g^y = 4³ = 9 mod 11
k = (h₁)^y = 3³ = 27 = 5 mod 11
c₂ = k × m = 5 × 5 = 25 = 3 mod 11

In practice, it is common for G, q, g to be standardized, fixed and shared.

Key Derivation and Private Key Encryption

We also assume the message m is a group element, which is rather inconvenient, because group might have some special representation and any arbitrary message might simply not correspond to some valid group element.

The simple solution is, rather than treating the message m as a group element and multiplying it by the key k, instead to use hash to derive another key and use the new key to encrypt the message m using private key encryption scheme. It is essentially hybrid encryption. So message does not have to be a group element any more, meanwhile, we also get the asymptotical efficiency of private key encryption.

k = Hash(h₁^y)
c₂ = PrivEnc_k(m)

CPA-Security

Theorem: if the Decisional Diffie-Hellman assumption is hard relative to the group generation algorithm ?, then the El Gamal encryption scheme is CPA-secure. It follows almost directly from the security of the Diffie-Hellman key exchange protocol.

As long as we are talking about the key exchange, the discrete logarithm assumption itself is not enough for public key encryption, we need some stronger assumption like the Computational Diffie-Hellman or Decisional Diffie-Hellman assumption.

CCA-Security

El Gamal encryption is not secure against Chosen Ciphertext Attack, i.e. it is NOT CCA-secure. This follow from the fact that the scheme is malleable. For example: transform c₂ by multiplying an arbitrary constant α in the group.

c₂' = α × c₂ = α × k × m = k × (α × m)

By transforming the cipher text c₂ to c₂', we were able to successfully transform the message m to (α × m). This is exactly a malleability attack.

However we can still obtain CCA security for El Gamal encryption scheme if we are a little bit careful in how we instantiate it when using key derivation. if we use key derivation with a CCA secure private key encryption scheme PrivEnc'_k, then El Gamal scheme can be proven to be CCA secure under appropriate assumptions that are actually stronger than the Decisional Diffie-Hellman assumption, also if Hash function is modeled as a random oracle, i.e. random mapping from group elements to the set of keys it outputs.

This approach has been used to construct the standardized encryption schemes DHIES based on subgroups of Z*_p and ECIES based on elliptic curve group.

RSA Based Encryption

Firstly, recall the RSA problem:

Choose two equal-length primes p and q at random.
Compute their product, the modulus, N = p × q.
Choose e, and d such that e × d = 1 mod φ(N).
We know that the e-th root of x modulo N is [x^d mod N].
(x^d)^e = x^de = x^{[ed mod φ(N)]} = x mod N

On the other hand, the RSA assumption is given N and e only (particularly d, p, q are not give), it is hard to compute the e-th root of a uniform element c in Z*_N.

CPA-Security of “Plain” RSA Encryption

The “plain” RSA encryption just based on the description above is not CPA secure. The “plain” RSA encryption scheme is deterministic, that is when you encrypt a message m, you always get the same cipher text, but any CPA secure encryption scheme must be randomized.

Worse, the RSA assumption only refers to hardness of computing the e-th root of a uniform element c. However c is not uniform unless the original m is uniform.

Furthermore the RSA assumption only refers to hardness of computing the e-th root of the element c in its entirety. It says nothing about whether it might be possible to compute partial information about the e-th root of c, even if c is uniform. In fact there are particular bits of information that is possible to learn about, which means the Information is being leaked about the message m, even if the message m is a uniform element of Z^*_N.

So, the plain RSA encryption should never be used!

PKCS #1 v1.5

This is a standard issued by RSA labs in 1993, tries to address some of the issues we mentioned previously by using random padding.

Bit length of message m is much smaller than that of the modulus N.
Choose a random bit string r of some prepend length.
Prepend r to the message m, view the concatenation as an integer in range of 1 to N-1.
Get cipher text c = [ (r|m)^e mod N ]

For example: N = 55, e = 3, m is 011 (3 bits), r is 10 (2 bits). The concatenation is 10011, which is 19 in decimal. c = [19³ mod 55] = [6859 mod 55] = 39, which is 100111 in binary.

This is good because it addresses the main deficiency of the plan RSA encryption (which was not randomized). Unfortunately there is no proof that this scheme with the padding is CPA-secure, unless the message is very short on the order of a small handful of bits.

In fact there are Chosen Plaintext Attacks known when r is too short. Even worse Chosen Ciphertext Attacks are also known.

PKCS #1 v2.0

In this new scheme, Optimal Asymetric Encryption Padding (OAEP) is used to transform the message before raising it to the e-th power. This padding introduces some redundancy, so that not every possible element in Z^*_N is valid cipher text, only some negligible fraction of the Z^*_N are actually valid. Upon decryption, the receiver actually needs to check for the proper formatting and return an error if the result is not properly formatted.

RSA-OAEP can be proven CCA-secure under the RSA assumption, if G andH are modeled as random oracles. This encryption scheme is widely used in practice.

My Certificate

For more on Public Key Encryption, please refer to the wonderful course here https://www.coursera.org/learn/cryptography

My #90 course certificate from Coursera

Related Quick Recap

Public Key Revolution

I am Kesler Zhu, thank you for visiting my website. Check out more course reviews at https://KZHU.ai