Securitization
Securitization is the process of constructing new securities from the cash flows generated by a pool of underlying securities. The economic rationale behind securitization is that it enables the construction of new securities with a broad range of risk profiles. A board range of investors may therefore be interested in these new securities even if they had no interest in the underlying securities. This results in the increased amount for the underlying cash flow, and in turn insures the cost-of-capital is reduced for the issuers of the underlying securities.
Credit Debt Obligations (CDO)
CDOs are securities constructed from an underlying pool of fixed-income securities. The underlying pool forms the collateral for the CDO, and which is then divided into tranches defined by their lower and upper attachment points. Investors can buy tranches and receive returns over the lifetime of the CDO, if none of the bonds in the underlying pool of assets defaults. But if some bonds default, then the tranches would have to incur the losses. That means investors will only receive less than expected, depending on the number of losses in the underlying pool of bonds.
If any losses arise that impact tranches, investors would have to pay some sort of payments because of those losses. In the case of Synthetic CDO, investors don’t buy a tranche, in fact the payments of a Synthetic CDO are structured to work like a swap, so no cash flows take place at the beginning of the trade. In practice, in order to construct the CDO, the banks that might only underline pool of bonds will often construct Special Purpose Vehicle.
If the underlying bonds were instead replaced with loans, it would be Collateralized Loan Obligations (CLO).
The mechanics of how CDOs work have much in common with the mechanics of Credit Default Swaps (CDSs).
Gaussian Copula Model
In order to price credit derivative and CDOs we need to compute the portfolio loss distribution. Knowing the distribution of the number of defaults is equivalent to knowing the distribution of the total loss in the reference portfolio. That is because L losses is equivalent to L times A * (1-R) in the portfolio of bonds. Knowing one implies the other. The assumption of constant A and R simplifies the calculation.
Conditional on the variable M, the total number of defaults is binomial distributed. But this holds only when correlation and default probabilities of all names are identical., respectively. Otherwise you will end up with different qM for each name in the portfolio.
When observing the relationship between ρ and expected loss with different default probabilities, you may find:
- The expected loss of equity tranche is usually larger than that of the mezzanine tranche, which is usually larger than that of the senior tranche.
- The expected loss in equity tranche is always decreasing in ρ.
- The expected loss in mezzanine tranche is usually insensitive to ρ.
If the senior tranche is with upper attachment 100%:
- The expected loss in senior tranche is always increasing in ρ.
- The total expected losses on the three tranches, i.e. the expected loses on the index, is independent of ρ.
- The allocation of the losses among all tranches depend on ρ.


Synthetic CDO Tranches
A tranche is defined by the lower and upper attachment points L and U respectively. Usually L and U are given as percentages of the total portfolio notional amount. The tranche loss function TLU,L(l) for a fixed time t, is a function of the number of defaults l, up to time t. The total portfolio loss is A * (1-R), which must be smaller than the upper appointment U. It tells us for a given number of defaults, what loss is suffered by tranche.
When an investor sells protection on the tranche she is guaranteeing to reimburse any realized losses on the tranches to the protection buyer. In return the protection seller receives a premium at regular intervals from the protection buyer. By protection, you might think of it as insurance.
The fair value of the CDO tranche is the value of the premium for which the expected value of the premium leg equals the expected value of the default leg. Just like a swap, the initial value of the position is zero. Clearly then the fair value of the CDO tranche depends on the expected value of the tranche loss function at each of the fixed time period.
Premium is payed on the outstanding notional of the tranche. Defaults causes losses which in turn decreases the notional of the tranche by amount of A * (1-R). So premiums get decreased after each default event occurs.
The big picture is as follows:
- We want to compute the fair value S of CDO tranche
- Compute the fair value of premium leg and default leg, set two legs equal and get value of spread S*.
- Compute the expected value of tranche loss.
The reason why Gaussian Copula model is popular is because it is easy to calculate expected value of tranche loss, even though the model itself has many flaws.

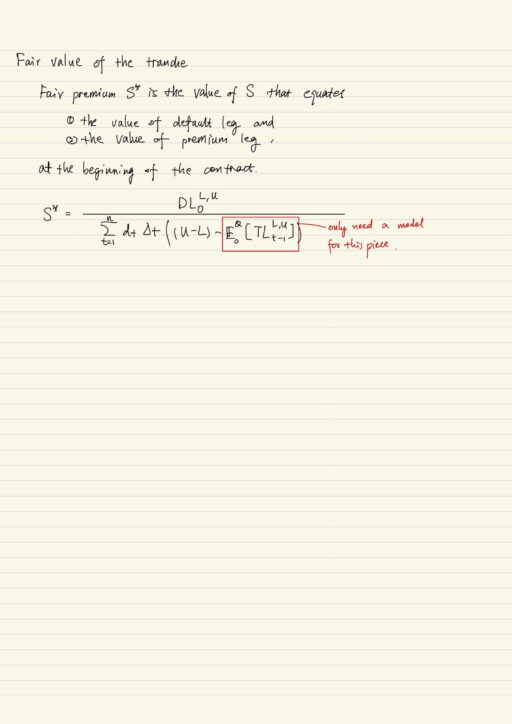
Cash CDOs
Cach CDOs are those where the reference portfolio actually existes and consisted of corporate bonds that the CDO issuer usually kept on its balance sheet. Capital requirements meant that these bonds required a substantial amount of capital to set aside to cover any potential losses
Banks want to reduce these capital requirements, they converted the portfolio into a series of tranches and sold most of these tranches to investors, and kept the equity tranches for themselves, therefore keeping most of the economic risk and rewards of the portfolio.
Cash CDOs must be managed, and the legal documentation can be lengthy. You get features like waterfall structures, credit enhancement, etc.
Synthetic CDOs
Once cash CDOs came into the marketplace, there was an appetite for these products. Hedge funds were keen to buy the riskier equity tranches (with the most risk and also greatest expected reward in the future). Insurance companies sought the AAA rated senior and super-senior tranches.
This appetite and explosion in the CDS market gave rise to so called synthetic CDO tranches, where the underlying reference portfolio is no longer a physical portfolio of corporate bonds or loans. Instead it is a fictitious portfolio consisting of a number of credits with an associated notional amount for each credit.
There are at least 2 features that distinguish synthetic CDOs from cash CDOs:
- With a synthetic CDO, it is no longer necessary to tranche the entire portfolio and sell the entire “deal”.
- Because bank no longer owns the underlying bond portfolio, it is no longer hedged against adverse price movements. It therefore needs to dynamically hedge its synthetic tranche position using CDS markets.
Risk Management of CDO Portfolios
In practice, structured credit portfolios could contain many many positions with different reference portfolios, different maturities and counter-parties. or different formats (i.e. upfront format and / or a running spread).
The ultimate payoff of a portfolio is very path-dependent with substantial idiosyncratic risks. They are very difficult to risk manage and very expensive to unwind due to wide bid-offer spreads. Current price should be interpreted as mid point of a bid-offer spread. So the bid on the offer would be on either side (selling on the left, buying on the right). Computing the mark-to-market price of these portfolios can also be very difficult, because market price can be non-transparent. Mark-to-market is referring to the current value of the portfolio using current prices in the market prices.
The risk management of structured credit portfolios is very challenging:
| Scenario analysis | Stress important risk factors for portfolios. 1. What is the main risk factor? Overall credit spreads, individual credit spreads, correlation… 2. What are the reasonable level of stress? 3. How to re-evaluate the portfolio in a given scenario? It is hard to find a good model. Gaussian Copula is a flawed model. |
| Greeks | They don’t work well and are model dependent. |
Liquidity risk and market endogeneity are also key risks must be considered. Market endogeneity means if everybody holds the same position, that is a much risker situation to be in, than if only a few people hold a position. Imaging when everyone is exiting and selling a stock, the price will collapse.
Copula Models
Gaussian Copula model is the most famous model for pricing structured credit securities. There has been enormous criticism aimed at this model. It is a static model, there Is no dynamics in the model. We just compute the expected tranche loss given a fixed period of time. There is no stochastic process there, we assume credit spreads are constant. We assume correlation is constant across various names. There are problems with time consistency.
A common fallacy is that the marginal distributions and correlation matrix are sufficient to describe the joint distribution of a multivariate distribution. This is not true. Correlations only measure linear dependence.
CDO-Squared
CDO-Squared were difficult to justify economically. and provide a great example of:
- product risk: people don’t really understand the product they are purchasing
- model risk: models were completely inadequate for pricing these securities
- legal risk: the actual contracts under these CDOs are many thousands of pages.
CDO-Squared is actually constructed from tranches of the underlying CDOs.
My Certificate
For more on Credit Derivatives and Structured Products, please refer to the wonderful course here https://www.coursera.org/learn/financial-engineering-2
Related Quick Recap
I am Kesler Zhu, thank you for visiting my website. Checkout more course reviews at https://KZHU.ai
