Linear homogeneous differential equation is the second-order ODEs that has the form below, It is important that the function p and q do not depend on x and any of its derivatives:
d2x/dt2 + p(t) dx/dt + q(t) x = 0A second-order homogeneous ODE with constant coefficients takes the form below, where a, b and c are constants.
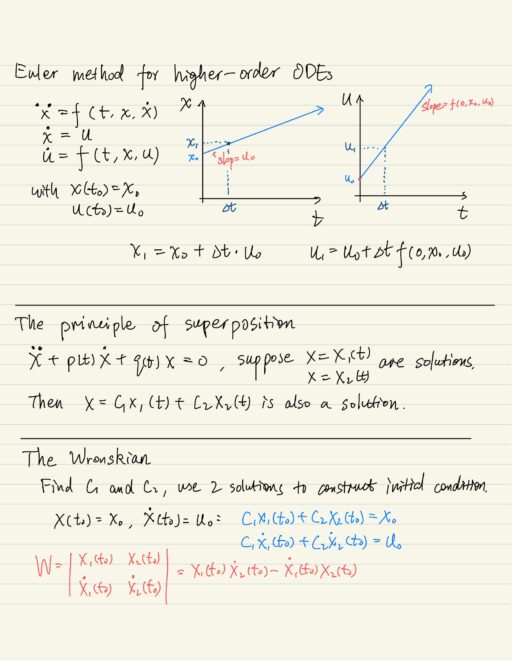
a d2x/dt2 + b dx/dt + c x = 0Euler Method for Higher-Order ODEs
Second-order equation for x, which is a function of time ti, can be written in some general form:
x'' = f(t, x, x')The idea to solve a second-order equation is to write it as a system of two first-order equations, and then we apply Euler method to the first order equations. Define a new variable u = x’ . Then x” = u’ .
x' = u
x'' = u' = f(t, x, u)
# initial condition required
x(t0) = x0
u(t0) = u0Euler method tells us then we step ∆t long the direction of the slope (the tangent of the curve), find the new point.
The Principle of Superposition
For a second-order linear homogenous differential equation, the principle states that if we have 2 solutions, their linear combination is also a solution.
x = c1 X1(t) + c2 X2(t)The Wronskian
We would like the superposition of two solutions to be the general solution of the differential equation. By a general solution, it means by choosing suitable c1 and c2, we can satisfy the two initial conditions. We try to construct a linear system with 2 equations and 2 unknowns. When we can do that is indicated by the name of Wronskian, we need Wronskian ≠ 0.
Wronskian is actually the determinant of the matrix of the linear system we built. If it is not equal to 0, then there is a unique solution to the equation system.
Homogeneous Second-Order ODE with Constant Coefficients
We can write the general equations as:
a x'' + b x' + c x = 0 We are going to look for 2 solutions that have a non-zero wronskian so we can satisfy two initial conditions. By using ansatz method, we are going to guess the form of the solution that has a free parameter. And by substituting into the differential equation, we are going to determine the free parameter.
We’d like to convert the differential equation into an algebraic equation. The proper ansatz here will be an exponential function. And the free parameter here actually should go in the exponential function, so let’s try the function x(t) = ert , where r is the unknown parameter and we hope substituting this ansatz into the differential equation, we will end up an algebraic equation for r.
There are 3 possible cases for the algebraic equation for r:
| b2 – 4ac > 0 | distinct real roots |
| b2 – 4ac < 0 | complex-conjugate roots |
| b2 – 4ac = 0 | repeated (degenerated) roots The ansatz found only 1 solution, it failed to find the second solution. The easiest way to find the missing solution is to start from the two complex conjugate solutions |
For the repeated roots, the easiest way to find the missing solution is to start from the two complex conjugate solutions, and see what happens when you take the limit that the imaginary part of the root of the characteristic equation goes to zero.
My Certificate
For more on Homogeneous Linear Differential Equations, please refer to the wonderful course here https://www.coursera.org/learn/differential-equations-engineers
Related Quick Recap
I am Kesler Zhu, thank you for visiting my website. Check out more course reviews at https://KZHU.ai
All of your support will be used for maintenance of this site and more great content. I am humbled and grateful for your generosity. Thank you!
Don't forget to sign up newsletter, don't miss any chance to learn.
Or share what you've learned with friends!
Tweet
