Special Relativity: Length and Simultaneity

The concept of “length” and “the same time” have to be reconsidered in special relativity.

---

---

Light Ruler and Length Contraction

In the example of the explosion of a grenade, it takes time ∆t from triggering to exploding. If it is triggered and immediately thrown with speed v, how long the grenade travels depends on your perspective:

Ground frame	If you put a ruler on the ground and observe the motion of the grenade, due to time dilation, the distance it travels is γ v Δt = v Δt 1/√(1 - v2/c2)
Grenade frame	Grenade itself is considered static now, but the ruler on the ground is considered moving with respect to the grenade. The speed of ruler is still the same v. The distance it travels is v Δt.

Four-Step Reasoning

Step 1 is to define the device. Firstly, we can have a light clock to measure time; secondly, we know that the speed of light is a constant of nature, which is independent of different inertial frames. We can define length as a light ruler, using the light clock, an emitter, a detector and a mirror. The light clock is used to measure the time Δt, starting at the moment that the emitter emits a light, which is reflected on the mirror and goes back to the detector. The time duration Δt ends at the moment that the light reaches the detector. Then we can define the length of the ruler as D = c Δt / 2.

Step 2 is to load the device light ruler onto a “car” with Alice inside. The car is moving with speed v. Alice is not looking outside the car, she will find nothing strange. The length of light ruler with respect to Alice should be the same as the rule is on the ground: DA = c ΔtA / 2.

Step 3: Draw spacetime diagram for Bob, there are 3 key events:

1. tB = 0: the emitter emits the light. The time .
2. tB = ∆tB1: the light reaches the mirror.
3. tB = ∆tB2: the light reaches the detector.

The length of the ruler with respect to Bob is DB = (c - v) ∆tB1 = (c + v) ∆tB2. We can solve ∆tB1 = DB / (c - v) and ∆tB2 = DB / (c + v). Also ∆tB = ∆tB1 + ∆tB2 = γ ΔtA = 2 c DB / (c2 - v2). We can finally get:

DB = DA / γ = DA √(1 - v2/c2)

D_A is the length of the ruler with respect to a co-moving observer (Alice), D_B is the length of the ruler with respect to a static observer (Bob). The static observer will find that the length of the ruler has been contracted because γ ≥ 1.

Step 4: One ruler is for all rulers. It does not matter whether the light ruler is used, any ruler (such as conventional ruler or your arm as a ruler) will work. If there exist a ruler that does not agree with the light ruler, Alice will find herself moving without referring to the outside of the car, which contradicts the principle of relativity.

---

---

Light Speedmeter and Velocity Addition

Using the light clock and the light ruler together, we can measure velocity of a moving object. Let us use a setup very similar to the light clock, however:

1. the emitter emits a particle which is not light, but a particle with speed u.
2. at the moment that the particle reaches the mirror, the mirror send backs a light with speed c.
3. the light reaches the detector.

Then ∆t1 = D / u, ∆t2 = D / c, and ∆t = ∆t1 + ∆t2, which can be measured by light clock. Also D can be measured by light ruler, c is a constant, then we can calculate u:

∆t = D (1/u + 1/c)
⟹ u = 1 / (∆t/D - 1/c)

It is useful to load the light speedmeter on a “car” and we can measure the speed of the particle with respect to different observers. The car is moving, the particle is also moving, its Velocity Addition.

Four-Step Reasoning

Step 1 is to define a device called light speedmeter, just described above.

Step 2 is to load the device light ruler onto a “car” with Alice inside. The car is moving with speed v. Alice is not looking outside the car, she will find nothing strange when using the light speedmeter. ∆tA = DA (1/uA + 1/c). She can calculate u_A.

Step 3: Draw spacetime diagram for Bob, there are 3 key events:

1. tB = 0: the emitter emits the light. The time .
2. tB = ∆tB1: the light reaches the mirror.
3. tB = ∆tB2: the light reaches the detector.

The length of the ruler with respect to Bob is DB = (uB - v) ∆tB1 = (c + v) ∆tB2. We can solve ∆tB1 = DB / (uB - v) and ∆tB2 = DB / (c + v). Also ∆tB = ∆tB1 + ∆tB2. Finally we can get the velocity addition rule in special relativity:

uB = (uA + v) / (1 + uA v / c2)

When uA = c, uB = c as well. So the speed of light is invariant for all inertial observers.

Terrell Rotation

Previously when we talk about the Twin Paradox, we are talking about the time in one’s frame (the coordinate time). It means we project the time of the two events to the time axis of an observer and then compare them.

Similarly, when we talk about length, it is length in one’s frame, not the length exactly seen when the light signal propagates to observer’s eyes. In practice, all objects have three dimensions: length, height, and depth in different directions.

Because the speed of light is finite, different points on an object has different distance to an observer, the light emitted from a farther point will takes more time to arrive at observer’s eyes than the light emitted from a nearer point. So the object appears that it is rotating, an observer sees different directions of an object at the same time.

We need to be careful when saying moving objects appear to be shorter. When we say “appear to be shorter”, it actually means the length in one’s frame, NOT the length to one’s eyes. If we talk about a sphere which is moving in front of us, the light that comes to our eye will let the sphere appears exactly as a sphere.

---

---

Same Time

Time dilation means that the time duration between two events will be different with respect to different observers if the observers have relative motion. This actually forces us to reconsider the concept of simultaneity, i.e the concept of what do we mean by two things happen at the same time.

The original concept of same time in our mind is actually wrong, because our motion is very slow compared to the speed of light, we don’t have to think much carefully. However, in special relativity, where we are talking about motion speed comparable to the speed of light, we have to be very carefule about what we mean by “the same time”.

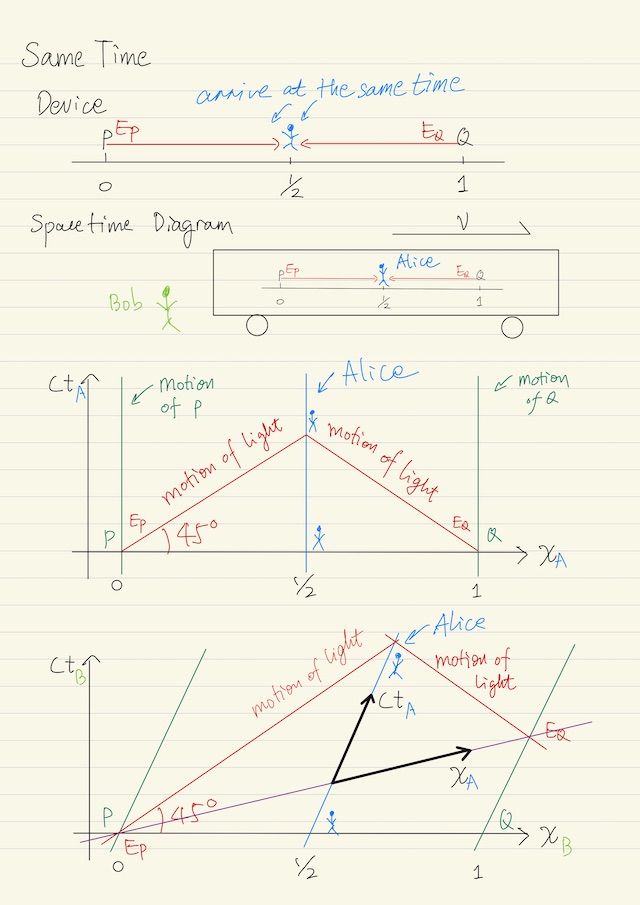
Device for Same Time

We just define the same time using a practical physical device. We use local concept of same time (small space and small time duration of the observer) to define the global concept of the same time (two events far far away to each other):

1. An observer is standing at the middle of the two places: P and Q, which have been there for long time.
2. There is a moment that an event E_P happens at the place P. Similarly there is a moment that an event E_Q happened at the place Q.
3. If the light signal coming from E_P and the light signal coming from E_Q reach the observer at the same time, then E_P and E_Q are considered happened at the same time.

Spacetime Diagram

Originally, in a spacetime diagram, the horizontal axis x is the space, the vertical axis t is the time. But if we multiple the time t by light speed c, and make it ct, which is the same dimension as the space x. In such a way, we are actually drawing the spacetime diagram in the same dimension x, then we can make sense of the slope of the line in geometrical sense.

1. Events E_P and E_Q are points on the spacetime diagram.
2. Lights travel in lines of 45 degree. (Once we have normalized the vertical axis ct).
3. Moving objects travel in lines of > 45 degrees, as long as the speed of the motion of the objects is smaller than the speed of light.
4. Inertial observers correspond to straight lines. (For every point, the speed is the same).
5. Static observers correspond to vertical lines.
6. If two events happened at the same time, they are on the same horizontal line.

Relativity of Same Time

We are loading the same time device on a car with Alice. But Bob is standing on the ground and sees. The two events, which happen at the same time with respect to Alice, are not happening at the same time of Bob. The concept of the same time is relative with respect to different observers.

---

---

Twin Paradox (Again)

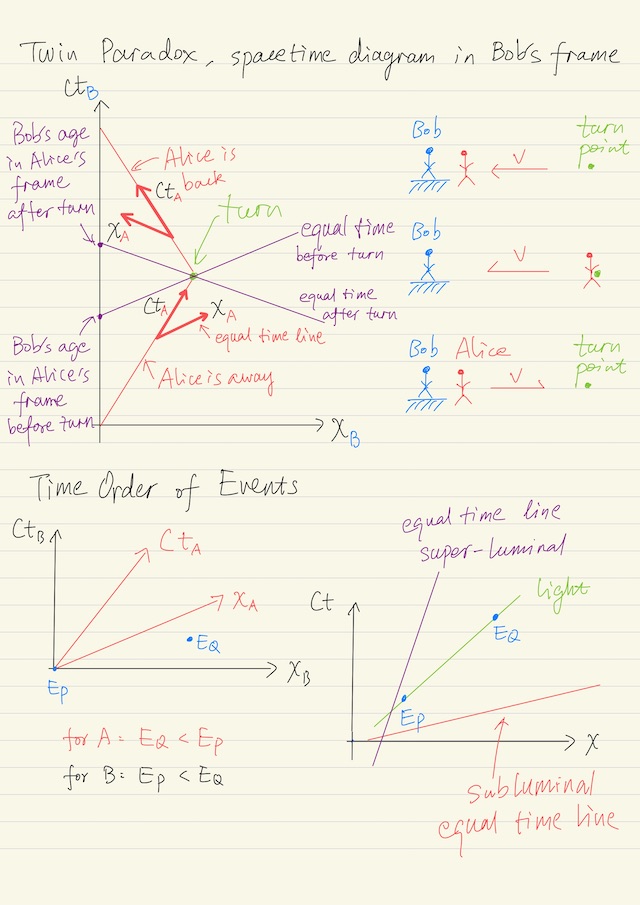
Alice and Bob are twins, initially they have the same age. Alice is moving in a direction with extremely fast speed close to speed of light. At a point, Alice turn around and go back. Alice will find that she is younger compared to Bob. The interpretation of this twin paradox is that Bob is always in inertial frame, so we can rely on Bob’s calculation about the aging of Alice. The twin paradox can be depicted in the spacetime diagram of Bob’s frame. At the time when Alice turn around (in Alice’s frame), the frame time of Bob suddenly get older. This is how to interpret twin paradox in Alice’s frame with the help of the spacetime diagram in Bob’s frame.

All the time that we are talking about is the time in Alice frame. It is not exactly the light wave of the image of Bob that come to Alice’s eyes. If you want to talk about the image of Bob coming to Alice’s eyes, you have to also consider that the speed of light is finite. So there needs time for the light wave to travel to Alice’s eyes. In this case, there is a continuous process for Bob getting old instead of at the turning point that Bob suddenly gets older.

Time Ordering of Events and Causality

For the time ordering of two events, it is possible that event E_P is earlier than E_Q with respect to one observer, and event E_P is later than E_Q with respect to another observer. The time order of events may be relative compared to different observers. If that is possible, that will be a disaster for us, because the the foundation of science known as “cause and effect” has changed, everything of our understanding had to be rethought.

An example of “cause and effect”: E_P = A thunder hits a tree. E_Q = The tree dies. The thunder causes the death of the tree. In the frame of the tree, E_P happens first, E_Q happens next. If you draw a line connecting E_P and E_Q, the line should be > 45 degree, which means sub-lunimal, i.e. the motion of the observer (corresponding to the line) is slower than light. It is impossible for the line to have < 45 degree, which is super-luminal.

Now the question is, is it possible to find out a reference frame in which E_Q happens first (tree dies) and then E_P (the thunder hits the tree)?

1. (Sub-luminal) As long as an observer is not faster than the speed of light (> 45 degree) , the equal time line (< 45 degree) will always touch E_P first and then E_Q.
2. (Super-luminal) However if an observer can move faster than the speed of light (< 45 degree), the equal time line bends over the speed of light (> 45 degree), E_Q will happen first, then E_P.

If we assume that everything is moving not faster than light, then causality is preserved in special relativity. We can classify the possible relations between two events into 3 classes:

Space-like	1. Line connecting two events < 45 degree. 2. Inertial observers always exist whose space axis is space-like. 3. Time order of events can be flipped by considering different observers. 4. Two events on a space-like line can not have cause and effect relation.
Light-like	1. Line connecting two events = 45 degree (trajectory of light). 2. The boundary of the light cone.
Time-like	1. Line connecting two events > 45 degree. 2. Inertial observers always exist who are not moving, and can connect 2 events on a time-like line (just the time development).

---

---

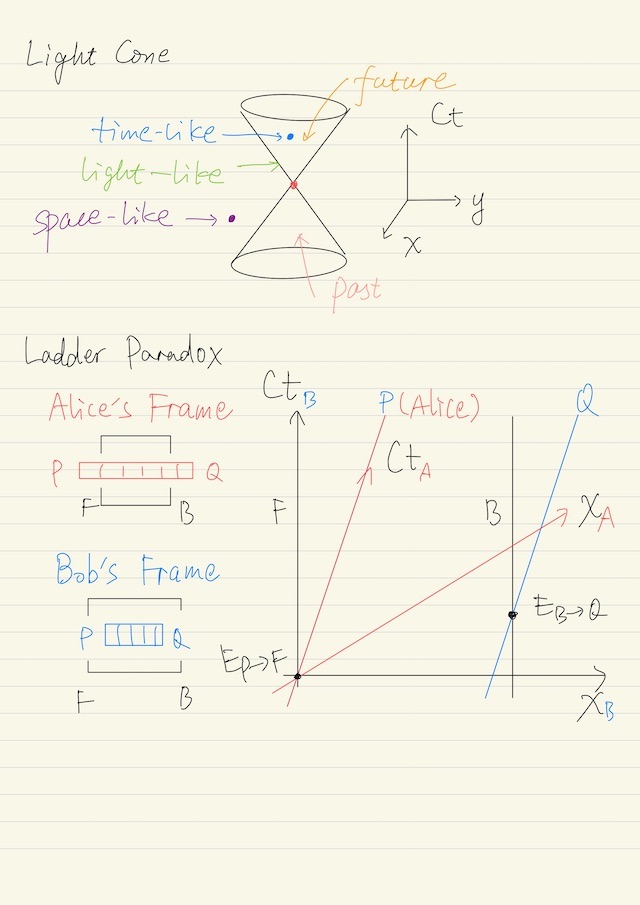
Light Cone

If we extend the spacetime diagram to 3 dimension, we get light cone.

1. The boundary of the light cone is the light-like separations.
2. Every point inside the light cone has time-like separation to the point in the middle.
   • Past light cone: points in past light cone could possibly be the causes of the point in the middle.
   • Future light cone: points in future light cone could possibly be the effects of the point in the middle.
3. Every point outside the light cone has space-like separation to the point in the middle.
   • There is no cause and effect relation.

Perfect Rigid Body

In special relativity, no perfect rigid body is allowed. The motion of part of material is restricted by the speed of sound in the material and further restricted by the speed of light.

Ladder and Garage Paradox

Assuming that Alice is moving together with a ladder which is 3 meters if at rest in Alice’s frame. Alice is moving to Bob’s garage, which is also 3 meters long. Alice and Bob has different perspectives:

1. In Alice’s perspective, she considers the garage is moving, and the moving garage has contracted.
2. In Bob’s perspective, he thinks the ladder is moving, and the moving ladder has contracted.

To mathematically define the question, there are 2 key events. Now the question “if the ladder fits the garage” converts to “which of the events happens first?”

EP→F	The left end of the ladder P enters the front gate F. This event happens first, if the ladder fits the garage. (Bob’s perspective)
EB→Q	The right end of the ladder Q leaves the back gate B. This event happens first, if the ladder does not fit the garage. (Alice’s perspective)

Both of Alice and Bob are correct.

---

---

My Certificate

For more on Special Relativity: Length and Simultaneity, please refer to the wonderful course here https://www.coursera.org/learn/understanding-modern-physics-1-relativity-and-cosmology

My #100 course certificate from Coursera

---

Related Quick Recap

Special Relativity: Space and Time

---

I am Kesler Zhu, thank you for visiting my website. Check out more course reviews at https://KZHU.ai