Pure and Mixed Ensemble / State
In quantum mechanics, we only talk about average or expectation value for a physically observable quantity by taking multiple measurements on ensemble and taking average. Ensemble means a collection of identically prepared physical system. The Stern-Gerlach experiment is an example of producing an ensemble – a collection of electrons that all have a well-defined spin state up along the z direction (after the apparatus).
But how to describe the collection of electrons just coming out of the thermal source and before the apparatus? They have all randomly oriented spins. The most general description of a spin can not resolve this problem. Recall it is a superposition of |+⟩ and |-⟩, which are the basis vectors representing the spin-up and spin-down states:
|α⟩ = c+|+⟩ + c-|-⟩The state |α⟩ has a well-defined orientation once you fix the value of c+ and c-. So |α⟩ can not describe an ensemble (collection of electrons) with randomly oriented spin. We need fractional populations, for example an ensemble where 50% of the electrons are in spin-up state, and 50% are in spin-down state:
w+ = 50%, w- = 50%| Pure ensemble | Coefficients c+, c- are complex numbers Specify the phase relationship between |+⟩ and |-⟩An ensemble / state in which all members are described by the same state ket is called a pure ensemble / state. |
| Mixed ensemble | Fractional weights w+, w- are real numbers: ∑i wi = 1Do not carry any phase information Incoherent mixture An ensemble / state in which all members can NOT be described by a single state ket, and must be described in terms of fractional weights is called a mixed ensemble (state) |
Ensemble average
Suppose we are making a measurement on a mixed ensemble of some observable quantity A. The ensemble average is below, where wi is the fractional weight of state |αi⟩, which can be further described as superposition (ca’ is the coefficients) of the eigenkets |a'⟩ of observable A. The probability of finding the state |α(i)⟩ in a particular eigenket |a'⟩ is given by |ca'|2.
[A] = ∑i wi ⟨α(i)| A |α(i)⟩ = ∑i ∑a' wi |ca'|2 a'= ∑i ∑a' wi |⟨a'|α(i)⟩|2 a'
|α(i)⟩ = ∑a' ca' |a'⟩
ca' = ⟨a'|α(i)⟩Density operator
In case we choose a general basis set {|b'⟩}, which is not necessarily the eigenkets of A, we could express the average ensemble as the trace of a matrix:
[A] = ∑b' ∑b" ⟨b"|ρ|b'⟩⟨b'|A|b"⟩ = ∑b" ⟨b"|ρA|b"⟩ = tr(ρA)ρ is the density operator, defined as ρ = ∑i wi |a(i)⟩⟨a(i)|. Recall trace is independent of the choice of the basis set. You could choose whatever basis that is the most convenient. The density operator is Hermitian, and if normalized, its trace equals to 1. A pure ensemble is specified by wn = 1 for some certain value n and = 0 for all others, thus density operator is written as ρ = |a(n)⟩⟨a(n)|.
For a density operator, if you choose different basis sets, their matrix representation will look different.

Time Evolution of Density Matrix
Time evolution of a pure state |a(i)⟩ is given by time-dependent Schrödinger equation, suppose |a(i)⟩ could be expressed in terms of an orthonormal basis set {|b'⟩}, then putting in the density matrix, thus the time evolution of density matrix could be written as:
∂ρ/∂t = -1/ih [ρ, H^]This equation is also called Liouville equation, it tells you how a mixed ensemble evolve over time.
Indistinguishability
In classical physics, one can in principle track individual particles accurately even if they look alike. However, in quantum mechanics, particles are fundamentally indistinguishable, because tracking particles would mean that you have to make position measurements, which unavoidably disturb the system (related to uncertainty principle).
The two-particle system wavefunction can be expressed as a product of the two one-particle wavefunctions. In order to account for the two possibilities, the most general form of the wavefunction must be a linear combination of two possibilities. The fact that the two electrons are truly indistinguishable means that there is no difference when we swap the two electrons in our wavefunction.
We can not measure the wavefunction directly, but we can measure the probabilities. What needs to be invariant is the probabilities, i.e.: the absolute value squared of the wavefunction.
Permutation operator
The operators that rearrange particles are called the permutation operators. The simple operator that swaps two electrons are defined as P12, such that:
P12 |ψtotal(r1, r2)⟩ = |ψtotal(r2, r1)⟩ = γ |ψtotal(r1, r2)⟩And obviously, P212 = I, identity operator; and γ has only two possible values 1 or -1.
Bosons and Fermions
In general a system of identical particles is in an eigenstate of permutation operator.
| Bosons γ = +1 | Photons and all particles with integer spins. Bosons are symmetric under permutation (exchange) of two particles. |
| Fermions γ = -1 | Electrons and all particles with half-integer spins. Fermions are anti-symmetric under permutation (exchange) of two particles. |
No two fermions can occupy the same single-particle state (Pauli’s Exclusion Principle). But many bosons can occupy the same single-particle state.

Exchange Energy
In a two-electron system with identical spin states, the Hamiltonian is given as:
H^ = -h2/2m0 (∇2r1 + ∇2r2) + 1/4πε0 e2/|r1 - r2|Since electrons are fermions, the total wavefunction for the two-electron system can be expressed as a linear (anti-symmetric) combination of the products of the two single-electron wavefunctions.
|ψtotal⟩ = 1/√2 (|1,a⟩ |2,b⟩ - |2,a⟩ |1,b⟩)When calculating the expectation value of energy ⟨E⟩, classically we expect kinetic energy for electron 1 and 2, and also Coulomb potential energy between electron 1 and 2. However the ant–symmetric combination used in constructing the total wavefunction leads to additional terms: exchange energy, which has to do with the permutation (or exchange) of electrons.
Exchange energy is appreciable only when there is an appreciable overlap between the two single-electron wavefunctions. Exchange energy is a quantum mechanical phenomenon without classical analogy.
When we construct the anti-symmetric combination as above, we ignored spin by assuming the electrons have the same spin state, this is why electrons’ spatial state has to be anti-symmetric. Ignoring the spin-spin interaction, the Hamiltonian operator acts only on the spatial wavefunctions and thus the energy depends only on the spatial parts. If we include the spin state, we need to consider two cases:
| Case | Spin state under exchange | Spatial wavefunction | Total |
| Spin singlet | Anti-symmetric|x1⟩|x2⟩ - |x2⟩|x1⟩ | Symmetric | Anti-symmetric |
| Spin triplet | Symmetric|x1⟩|x2⟩ + |x2⟩|x1⟩ | Anti-symmetric | Anti-symmetric |
The two cases will produce exchange energies with opposite signs, which results in energy level splitting. Bosons also produce exchange energy, which however is negligibly small and they rarely become important.

Thermal Distribution of System of Particles
When extending system of identical particles to more than two particles (many-particle system), the total wavefunction is constructed with the products of individual one-particle wavefunctions as before.
Bosons
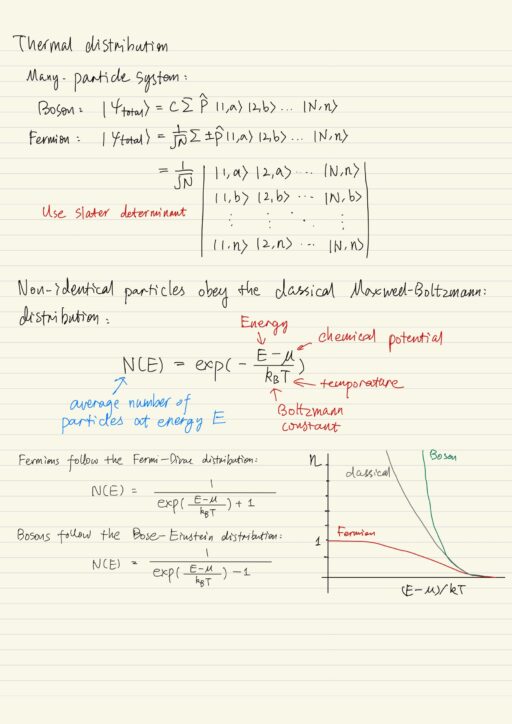
For a system of N bosons, the total wavefunction must be symmetric under exchange of any two particles, which can be obtained by |ψtotal⟩ = c ∑ P^ |1,a⟩ |2,b⟩ ... |N,n⟩, where the summation is over all possible permutations of particles. So there will be a total of N! terms in the summation. Swapping two particles means merely changing the order of permutation.
It is also possible that two or more particles occupy the same single-particle state, i.e.: a = b. There is no cancelation among terms.
Fermions
For a system of N fermions, the total wavefunction must be an anti-symmetric combination under exchange of any two particles: |ψtotal⟩ = 1/√N ∑ ±P^ |1,a⟩ |2,b⟩ ... |N,n⟩, where ±P^ means we are changing sign depending on the number of pairwise permutation:
- Add the terms corresponding to even number of pair-wise permutations.
- Subtract those corresponding to odd number of pair-wise permutations.
This procedure ensures the total wavefunction is anti-symmetric. If any two particles occupy the same single-particle states, the wavefunction is identically zero, because the permutation of the two particles results in two identical terms with opposite sign. This construction of the wavefunction satisfies Pauli’s Exclusion Principle as it shifts. A convenient way of constructing anti-symmetric wavefunction is to use the Slater determinant.
NOTE that the interaction among particles are weak is the reason why we could assume that we could express the total wavefunction of N-particle system by a linear combination of product of single-particle wave functions. If there is strong interaction among particles, you really can not use this method.
Thermal distribution
In classical physics, all particles are non-identical (distinguishable) particles, they obey the classical Maxwell-Boltzmann distribution. In quantum physics, fermions follow the Fermi-Dirac distribution, and bosons follow Bose-Einstein distribution.
Bosons have higher probabilities of occupying the same state, while fermions are limited to at most one particular per state. Classical particles have mean occupation numbers between bosons and fermions.
My Certificate
For more on Quantum Mechanics: Ensembles and Identical Particles, please refer to the wonderful course here https://www.coursera.org/learn/foundations-quantum-mechanics
Related Quick Recap
I am Kesler Zhu, thank you for visiting my website. Check out more course reviews at https://KZHU.ai



