The real physical devices that implement computational models are always imperfect. It is not always possible to eliminate all of error sources in practice, however in many cases one could minimize the chances of their occurrence.
Classical Error Correction Theory
There are three main problems in classical error correction theory:
- Analyze errors occurring in a data channel, and describe them in terms of a math model.
- Encode information allowing data recovery in case of error occurrence.
- Create algorithms and procedures of error elimination.
Information channel is an important concept which refers to devices that transfer, storage and process of information. If the channel is noisy, we must learn how to describe the errors occurring in the channel mathematically. The black box test involves special testing signals being sent, then the statistical analysis of the received results will allow one to identify and classify the errors that could occur, and select methods for error correction.
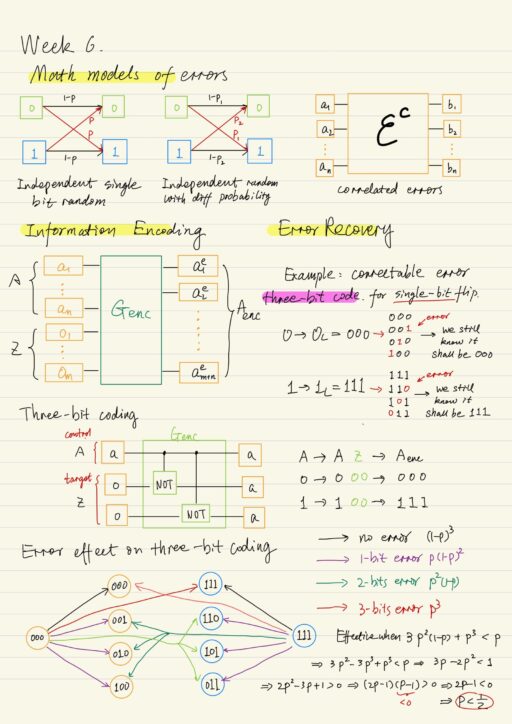
Mathematical models of errors
| Independent single-bit random | p: the probability for a bit-flip to occur in each bit. (1-p): the probability that no error occurs. |
| Independent single-bit random with different probabilities for different bit values | The bit-flip error probabilities are not the same for different bit values: p1: error probability for ‘0’ p2: error probability for ‘1’ |
| multi-bit correlated errors | Uncontrollable modification of several bits at once. Such errors are being schematically depicted as a logical element εc. |
The correction methods for these types of errors are based on the same principles.
Information encoding
The information encoding is based on the principle of redundancy, which includes the addition of extra bits and the creation of codewords, i.e.: the auxiliary bits are added to initial bits to form the codeword. The redundancy within information coding corresponds to a certain error type, which means that after part of information is corrupted because of errors, the rest part of information must be enough to restore the initial information. The channel’s quality determines whether a certain encoding method can be used or not.
Generally, the information encoding can be represented as an action of a certain reversible logical element Genc, by which the initial bit set A and the auxiliary bit Z are turned into a codeword Aenc after the encoding.
Error Recovery
The codeword is somehow destroyed when there is an error. We get Aerr instead of Aenc. So we need some special decoding procedure that will allow us to restore bitset A at least without restoring the auxiliary bitset Z. The decoding is possible if different codewords are different from each other after the affection of an error. Recall that the error affection can be considered as an action of a certain logical element ɛc on the codeword.
The correctable errors are those for which the code words Aenc and Benc remain distinguishable after the affection of errors ɛi and ɛj remain distinguishable:
ɛi(Aenc) ≠ ɛj(Benc), ∀ i,j ∈ {0,1,2,...,n}Classical Three-bit Code
The three-bit code relates to codes with repetition, i.e.: every bit 0 is replaced by a codeword of three 0s and every bit 1 value is replaced by a codeword of three 1s.
Recall that not all of the errors are correctable, a codeword encoded using three-bit coding could not be properly decoded if 2 bits have changed. For example codeword 000 becomes 101 as a result of 2 single-bit errors. Meanwhile 101 could also be a 1 single-bit error of the code word 111. In this case we can not tell which one of 000 or 111 was the initial codeword.
The three-bit code is effective only if the sum of probabilities of uncorrectable errors is less than the probability of correctable error: 3 p2 (1-p) + p3 < p which means p < 1/2, where p is the probability for a bit-flip to occur in each bit.
When restoring the initial codeword, the simplest method is to do bit-search and find the majority: the number of 1s or the number of 0s? For example: all codewords 100, 010, or 001 should have initial codeword 000. However this method of error correction is not effective in general case.
Parity comparison (XOR operation)
Instead of using bit-wise search and finding majority (at least 3 operations), in the case of three-bit code, it is enough to use only 2 logical operations:
- compare the parity of the first and the second bit, and then
- compare the parity of the first and the third bit.
Suppose the initial codeword is 000, the possible results include:
| No error | Parity of the first bit equals to the parities of ancillary bits. | 000 |
| Error in ancillary bits | Parity of the first bit matches only 1 of ancillary bits. | 010 or 001 |
| Error in the first bit | Parity of the first bit is different from ancillary bits. | 100 |
The parity checking provides one with enough information (also called the error syndrome) about errors occurred in the channel.

The features of Quantum systems
Firstly, the quantum evolution of a qubit (or a system of qubits) is a continuous physical process. In the real physical system, the logical operations are usually performed with a finite precision, and this will lead to errors despite the difference is small, thus the number of errors in general will be infinite. Instead of a point on the Bloch sphere, the situation corresponds to a certain area around this point, and there is an infinitely large number of quantum states in such area.
Secondly, as one measures the qubit being in a superposition of basis quantum states, the quantum reduction happens, and the superposition turns into one of the basis states. In order to use the qubit for further computation, one should not measure the qubit directly to find its state. Thus the error syndrome should be defined without direct measurement of the qubit.
Thirdly, according to the no-cloning theorem, it is impossible to create an identical copy of a qubit in an arbitrary quantum state.
Quantum Error Correction Theory
Like we did in the classical theory, there are 3 main problems of quantum error correction theory:
- Analysis of errors appearing in the information channel and their description via a math model.
- Encoding of information allowing one to restore in case of errors.
- Deployment of error correction procedures and algorithms.
The models of single-qubit errors
The physical environment of a qubit acts as a quantum information channel. The errors are considered as the result of the interaction between the qubit |ψ⟩ and the information channel |E⟩, which can be represented as |ψ⟩⨂|E⟩, also as a superposition of four discrete transformation.
| identity | α0|0⟩ + α1|1⟩ → α0|0⟩ + α1|1⟩ |
| phase error | α0|0⟩ + α1|1⟩ → α0|0⟩ - α1|1⟩ |
| bit-flip error | α0|0⟩ + α1|1⟩ → α0|1⟩ + α1|0⟩ |
| phase + bit-flip error | α0|0⟩ + α1|1⟩ → α0|1⟩ - α1|0⟩ |
This four errors don’t appear in a channel together always, it depends on the channel’s quality. Moreover, these errors can be represented by the Pauli matrices, because any single-qubit unitary operator can be represented by a linear combination of operators I, X, Z, Y (we have XZ = iY). A code that corrects the errors X, Z, Y allows one to correct any error that could be represented by their linear combination.
Information encoding
The encoding is based on the principle of redundancy as it was in the classical case. The encoding should proceed in such a way that if an error occurs and part of information is lost, the rest of information should be enough to restore the initial information.
Since the no-cloning theorem forbids us to create a copy of the qubit, we realize the redundancy principle using the quantum entanglement and proceed the further decoding. Quantum entanglement is being used in all of the quantum encoding schemes.
Error recovery
Not all of the errors are correctable, the quantum information channel should be developed with high accuracy. When the correctable errors occur, the different codewords |φenc⟩ ≠ |ψenc⟩ must be distinguishable in the channel.
The error correction operation must allow one to completely reverse the error affection or to transfer to the ancillary bits.

Quantum Three-qubit Code
Qubit-flip Errors
Three-qubit code allows one to protect the qubit in the state |ψ⟩ from the qubit-flip errors (with probability p). Quantum state of such a channel can be represented by a density matrix ρ with 2 terms, one for “no error” with probability (1-p), the other one for “qubit flip” with probability p.
ρ^ = |ψ⟩⟨ψ| → ρ^f = (1-p) |ψ⟩⟨ψ| + p X|ψ⟩⟨ψ|XThe codewords are:
|0⟩ → |000⟩
|1⟩ → |111⟩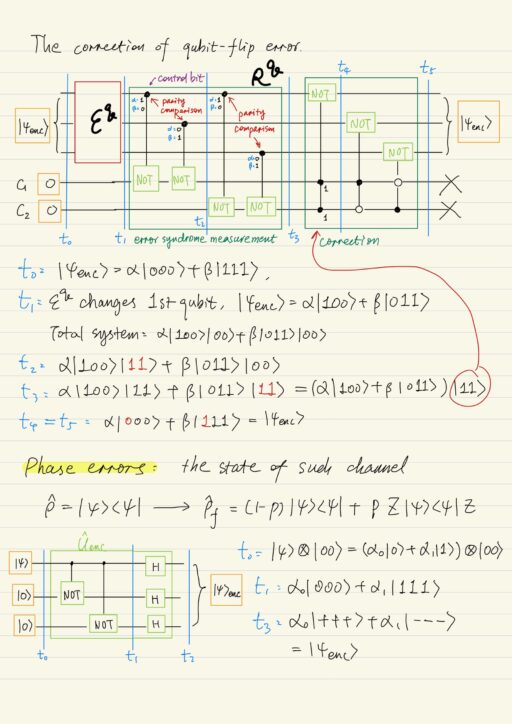
Phase Errors
If the phase errors occur in the channel, the three-qubit code could be used:
ρ^ = |ψ⟩⟨ψ| → ρ^f = (1-p) |ψ⟩⟨ψ| + p Z|ψ⟩⟨ψ|ZOne could correct the phase errors in the same way as qubit-flip errors using the Hadamard basis (via H).
|0⟩ → |+++⟩
|1⟩ → |---⟩The scheme for the correction of phase errors will be equivalent to the scheme for the correction of qubit-flip errors we’ve just considered, but with additional Hadamard elements for the change of basis.
Combined Errors (qubit-flip + phase error)
The three-qubit code is NOT enough and can NOT be used in this case. Instead the nine-qubit Shor’s code is used:
|0⟩ → 1/2√2 (|000⟩+|111⟩) ⨂ (|000⟩+|111⟩) ⨂ (|000⟩+|111⟩)
|1⟩ → 1/2√2 (|000⟩-|111⟩) ⨂ (|000⟩-|111⟩) ⨂ (|000⟩-|111⟩)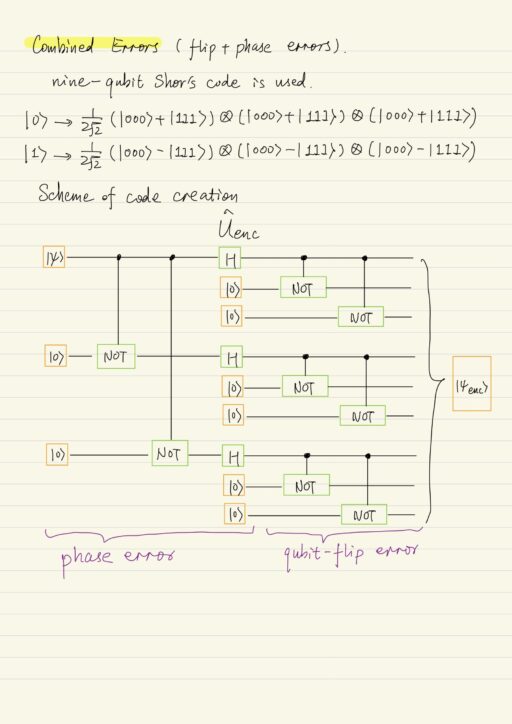
My Certificate
For more on Basics of Quantum Error Correction Theory, please refer to the wonderful course here https://www.coursera.org/learn/physical-basis-quantum-computing
Related Quick Recap
I am Kesler Zhu, thank you for visiting my website. Check out more course reviews at https://KZHU.ai