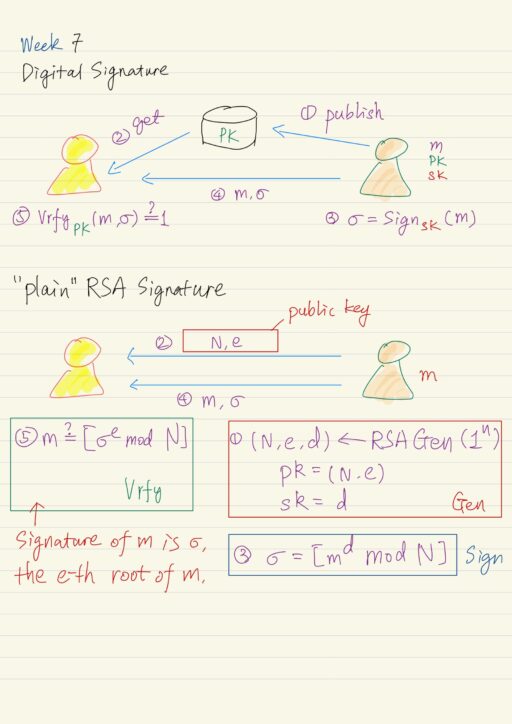
Digital Signature

Tweet

Digital signature is a mechanism that can be used to provide integrity in the public key setting, analogous to message authentication codes in the private key setting. However there is some key differences between the both.

---

---

How does digital signature work?

1. One party A locally generates a pair of public key pk and private key sk. They make the public key widely available.
2. Some other party B obtains a copy of the first party’s public key.
3. A authenticates a message m, by signing it using the private key sk, to obtain a signature σ = Signsk(m).
4. A sends the m and σ to B.
5. B could try to verify the signature on the claimed message, using A’s public key. Vrfypk(m, σ), if this outputs 1, then the receiver is assured that the message they received did originate at the claimed sender.

	Digital signature	Public key encryption
Sender	Party has the private key	Party has the copy of public key
Receiver	Party has the copy of public key	Party has the private key

The security goal is even after observing signatures on multiple message, an attacker should be unable to forge a valid signature on any new messages.

Compared to Message Authentication Codes

Digital signature is widely used for broadcasting patches for software. The goal is to prevent an attacker from modifying the patch, from giving a client a fake patch. The signature scheme will ensure that if the client verification fails, the client will simply reject the patch and refuse to install it.

However the Message Authentication Codes is not suitable in this scenario. Software distributor has to share the private key k with everyone who purchases a copy of the software. If any of the clients want to behave maliciously, there is nothing preventing the client from generating and authenticating their own patches using the same key k.

Digital signature has the property called “Public verifiability”. Which means anyone with public key can verify a purported signature from that sender. In the case of MACs, only a party who holds the matching key can do the verification. This actually has a number of very important consequences for signatures:

• Transferability
  • Can forward a signature to someone else.
• Non-repudiation.

---

---

Non-repudiation

Non-repudiation means sender can not (easily) deny issuing a signature. If they signed some message and released the message and the signature to somebody else, then anybody, who is able to very the message and signature, will be convinced that the original signer did indeed signed that message and issued that message.

This is crucial for legal applications. Judge can verify signature using the public key. Message Authentication Codes simply can not provide this functionality.

Signature Schemes

A signature scheme is defined by three probabilistic polynomial time algorithms:

Gen	Takes as input 1n (where n is the security parmeter). Outputs public key pk, and private key sk.
Sign	Takes as input a private key sk and a message m ∈ {0,1}*. Outputs signature σ ← Signsk(m).
Vrfy	Takes as input a public key pk, message m, and signature σ. Outputs 1 (valid) or 0 (invalid).

The correctness condition says that for all messages and all public private key pairs (output by the key generation algorithm Gen):

Vrfypk(m, Signsk(m)) = 1

Security

The security model for digital signature is like that for the message authentication codes. The threat model is “Adaptive Chosen-Message Attacks”, where we assume the attacker can induce the sender to sign messages of the attacker’s choice. The security goal is “Existential Unforgeability”, that is the attacker should be unable to forge a valid signature on any message not signed by the sender.

Formally,, fix a signature scheme Π, and some attacker A, we can define the randomized experiment ForgeA,Π(n):

1. Generate public and private key: pk, sk ← Gen(1ⁿ).
2. Give pk to the attacker A, who can interact with oracle Sign_sk(∙) by submitting messages and getting back the corresponding signatures; let M be the set of messages sent to the oracle.
3. A outputs a pair of message and its signature (m, σ).
4. A succeeds, and the experiment evaluates to 1, if Vrfy_pk(m, σ) = 1, and m ∉ M.

Π is secure if for all probabilistic polynomial time attackers A, there is a negligible function ε, such that:

Pr[ ForgeA,Π(n) = 1 ] ≤ ε(n)

Note the definition of this scheme does not take into account the Replay Attacks at all. This scheme does nothing preventing an attacker from taking a prior message signature pair, and replaying that to a recipient. This kind of attack need to be addressed using other mechanism like date, time or counter number.

---

---

Hash-and-Sign Paradigm

We’ve already seen this paradigm in the context of Message Authentication Codes. Actually not every Message Authentication Code uses this paradigm, for example CBC-MAC does not need to use any hashing before generating a message authentication code, whereas HMAC does that as part of its processing.

In the context of signatures, Hash-and-Sign is really ubiquitous. The basic idea is we are given:

1. A signature scheme Π = (Gen, Sign, Vrfy) for messages of length n.
2. A hash function H:{0,1}* → {0,1}ⁿ

then we can construct. a new signature scheme Π’ = (Gen, Sign’, Vrfy’) for arbitrary-length messages:

• Sign’_sk(m) = Sign_sk(H(m))
• Vrfy’_pk(m, σ) = Vrfy_pk(H(m), σ)

Theorem: if Π is secure and H is collision-resistant, then Π’ is secure.

Hash-and-sign paradigm is sort of analogous to Hybrid Encryption in the sense that it gives us the functionality of digital signatures at the asymptotic cost of a symmetric-key operation. If the message that you’re signing is very long, then the time to sign will start becoming dominated by the time to compute the hash over that long message. Hashing is a symmetric-key operation, so it is going to be very fast.

RSA Based Signature

Firstly, recall the RSA problem:

1. Choose two equal-length primes p and q at random.
2. Compute their product, the modulus, N = p × q.
3. Choose e, and d such that e × d = 1 mod φ(N).
4. We know that the e-th root of x modulo N is [x^d mod N].
   (xd)e = xde = x[ed mod φ(N)] = x mod N

On the other hand, the RSA assumption is given N and e only (particularly d, p, q are not give), it is hard to compute the e-th root of a uniform element c in Z*_N.

The “plain” RSA signature can be derived based on the RSA problem and RSA assumption above. It probably will give you an intuition that “because signature of message m (i.e. σ) is the e-th root of m, it should be difficult then for anybody only having the public key (e, N) to compute signature σ on message m. This intuition is completely wrong in several aspects:

1. Attack 1: It is easy to sign specific messages. For example it is easy to compute the e-th root of m = 1, i.e. 1 = 1^e mod N. The RSA assumption tells us that computing e-th root of random message m is hard, but it says nothing about the difficulty of computing e-th root of non-random messages.
2. Attack 2: An attacker is able to generate signature on random messages as often as he likes. An attacker can, with an arbitrary σ, let the message be determined from σ, i.e. set m = [σ^e mod N]. This would violate our definition of existential unforgeability, because attacker is able to come up with a signature on some message.
3. Attack 3: An attacker can combine two signature to obtain a third. Here attacker can in fact manipulate things so as to obtain a signature on any message of his choice. Say σ₁, σ₂ are valid signatures on m₁, m₂ with respect to public key N, e. Then attacker can obtain a new valid signature σ’ = [σ₁ × σ₂ mod N] on the message m’ = [m₁ × m₂ mod N]. Proof: (σ1 × σ2)e = σ1e × σ2e = m1 × m2 mod N. This is a really damaging attack that allows the attacker to potentially generate a signature on a message of his choice, as long as he can fool the signer into signing arbitrary messages of the attackers choice.

---

---

RSA-FDH Scheme

Now the RSA-FDH (Full Domain Hash) signature scheme was constructed exactly to prevent these kinds of attacks. The basic idea is to apply a “cryptographic transformation” to messages before signing like what we did in the “plain” RSA scheme.

We have private key d and public key (N, e) as before. When signing a message m, we compute, rather than e-th root of m itself, e-th root of H(m), for some cryptographic function H. It can also be verified easily, given a claimed signature σ on a message m, we compute H(m), and check whether σ is e-th root of H(m).

Signsk(m) = ( H(m) )d mod N
Vrfypk(m, σ) = 1 iff σe = H(m) mod N

This scheme actually naturally handled long messages, but this scheme is not an extension of the Hash-and-Sign paradigm. It just happens to have the side benefit of allowing the handling messages of arbitrary length.

How does RSA-FDH solve the 3 attacks exposed to the “plain” RSA signature?

1. Output of H is going to be some arbitrary value in Z^*_N, it is not specific anymore. So it is not likely to be easy to compute the e-th root of the output of H.
2. Calculating H(m) = σ^e mod N won’t give attack a message, it is just the hash of m, i.e. H(m). So in order to let RSA-FDH to be secure, it had better be difficult to compute inverse of H.
3. Multiplying 2 messages and 2 signatures to get a new message and signature pair is simply impossible, because (σ1 × σ2)e = σ1e × σ2e = H(m1) × H(m2) ≠ H(m1 × m2).

Solving these 3 attacks does not mean the scheme is secure, we still have to prove that there are no other attacks that can work.

Security

If the RSA assumption holds, and H is modeled as a random function mapping onto Z^*_N, then RSA-FDH is secure.

In practice, H is instantiated with a modified cryptographic hash function. From an implementation point of view, it’s not enough to simply take a cryptographic hash function off the shelf and use it here. The reason is that the range of typical cryptographic hash function is going to be too small. We must ensure that the range of H is large enough, such that the range of H is mapping roughly uniformly onto Z^*_N.

RSA PKCS #1 v2.1

The RSA PKCS #1 v2.1 standard includes a signature scheme that can be viewed as inspired by RSA-FDH. If signer uses no randomness, it is essentially RSA-FDH.

---

---

My Certificate

For more on Digital Signature, please refer to the wonderful course here https://www.coursera.org/learn/cryptography

My #90 course certificate from Coursera

---

Related Quick Recap

Public Key Encryption

---

I am Kesler Zhu, thank you for visiting my website. Check out more course reviews at https://KZHU.ai

Don't forget to sign up newsletter, don't miss any chance to learn.

Or share what you've learned with friends!

Tweet