Special Relativity: Geometry, Momentum and Energy

In 3-dimensional space, when we are looking at an object, what we see depends on the angle, the object is still the same object. Actually, the geometry of special relativity is nothing more than looking at a four-dimensional space-time object at different angles. We are actually looking at the relation of events at different angles, then we see space contraction and time dilation. But the fundamental relation of the events, the space-time interval, are still the same.

Space-Time Geometry

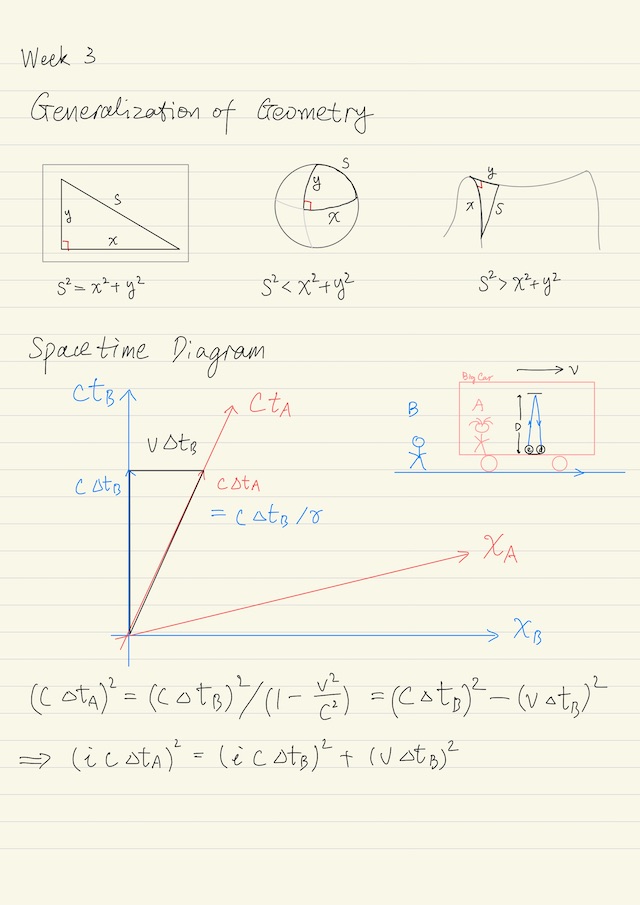
Time and space are unified into one thing called spacetime, Lorentz transformation tells us space and time can transform to each other. The geometry of an object can be studied by the Pythagorean theorem on this object. For example, a right triangle, we know the famous equation for hypotenuse s² = x² + y².

The Pythagorean theorem can also be generalized to 3-dimensions, where the curvature radius is different point-by-point. Because of the curvature of its surface, on a sphere, we have s² < x² + y². Or on a saddle, it is also possible to have the relation s² > x² + y².

The Pythagorean theorem can be further generalized to space-time, where one dimension is space, the other one is time. Suppose Alice is carrying a clock with her, and Alice is moving fast. Due to time dilation, we have c ∆t_A = c ∆t_B / γ in spacetime diagram. Then we can derive:

(c ∆t_A)² = (c ∆t_B)² / γ² = (c ∆t_B)² / (1 - v²/c²) = (c ∆t_B)² - (v ∆t_B)²
⟹ - (c ∆t_A)² = - (c ∆t_B)² + (v ∆t_B)²
⟹ (i c ∆t_A)² = (i c ∆t_B)² + (v ∆t_B)²

So, it seems if we put a factor of i in the time directions of Alice and Bob, we can use Euclidean geometry to help us understand Lorentzian geometry. The hyperbolic sin and cos functions are critical for us to further understand the geometry of relativity.

cosh(iθ) = cos(θ)
sinh(iθ) = i sin(θ)

Which are defined as below using exponential functions:

cosh(x) = 1/2 (e^x + e^-x)
sinh(x) = 1/2 (e^x - e^-x)
tanh(x) = sinh(x)/cosh(x)
cosh²(x) - sinh²(x) = 1

Rapidity

The rapidity ϕ is defined as the inverse function of hyperbolic tangent function of v/c:

ϕ = arctanh(v/c) = arctanh(β)

Similar to rotation, the rapidity functions can be added. This is great if you are unsatisfied with the velocity addition laws of relativity. For example, in 1-dimensional velocity addition problems, instead of the speed, you can consider ϕ_Bob = ϕ_Alice + ϕ_Object. Note that rapidity can be transformed to γ and β:

β = tanh(ϕ) ⟹ cosh(ϕ) = γ, sinh(ϕ) = βγ

Lorentzian Geometry

We could use rapidity ϕ to rewrite the Lorentz Transformation in another form, which really looks like the rotation in Euclidean dimensions. If we further redefine ϕ = i θ, and c t = i w, then we have:

Standard form Lorentz

c t_B = γ c t_A + β γ x_A
x_B = β γ c t_A + γ x_A

Rewritten Lorentz

c t_B = c t_A cosh(ϕ) + x_A sinh(ϕ)
  x_B = c t_A sinh(ϕ) + x_A cosh(ϕ)

Further rewritten Lorentz

i w_B = i w_A cos(θ) + x_A i sin(θ)
  x_B = i w_A i sin(θ) + x_A cos(θ)

Euclidean Rotation

x_A = x_B cos(θ) + y_B sin(θ)
y_A = -x_B sin(θ) + y_B cos(θ)

The transformation above reveals the fact that Lorentz Transformation is deeply related to Euclidean Rotation. If we make the time coordinate imaginary, i.e. c t = i w, then Lorentz Transformation is just rotation, and Lorentz geometry is Euclidean geometry.

Invariant Interval

Euclidean geometry can be represented in 4 dimensions as

ds² = dw² + dx² + dy² + dz²

In special relativity, w = -i c t, Lorentz geometry can be represented as

ds² = - d(ct)² + dx² + dy² + dz²

ds² actually has a very important geometrical meaning: the length of an interval. In the different frames, the components x, y, z, w could have different values. However, the length of the interval is independent of which frame you are looking at, it is invariant under rotation.

ds², i.e. the space-time interval, in special relativity is also invariant. The essence, most important thing in relativity is what is invariant under the transformations:

The vacuum speed of light is invariant for all inertial frames.
The laws of nature are invariant for all inertial frames.
The events happened or not are invariant for all inertial frames.
The causality, the cause and effect relation, is invariant.

Relativity is really about invariants and ds² is the mathematical formula for invariants.

space-like	`ds² > 0`
light-like	`ds² = 0` (null interval)
time-like	`ds² < 0`

Momentum

Momentum and energy are conserved quantities. Why they are conserved quantities? They can be derived by the symmetry of nature. Conserved quantities are of particular importance in the study of physics. There are a few reasons why we want to study conserved quantities:

From a physics perspective, we only care about initial state and final state. Given initial state, the conserved quantities (momentum and energy) are essential to calculate and predict the final state.
From a math perspective, it reduce a second order differential equation, into first order.
In modern physics, we are studying extremely fast (light), small (atom) and early (universe) conditions or processes, we have to rely one some conserved quantities.

Newtonian Momentum

Recall Newton’s momentum conservation law can be represented as:

m₁v₁^A + m₂v₂^A + ... = m₁v₁^'A + m₂v₂^'A + ...

In the equation, A means Alice’s frame. Now suppose we want to change to Bob’s frame in Newtonian mechanics, we need to use Newtonian velocity addtion law to transform all of the velocity v_i in Alice’s frame to v_i in Bob’s frame, i.e. v_i^B = v_i^A + v. And at last in Newtonian mechanics, the momentum conservation law in Bob’s frame does not change its form:

m₁v₁^B + m₂v₂^B + ... = m₁v₁^'B + m₂v₂^'B + ...

However, recall the velocity addition law in special relativity:

v_x^B = ( v_x^A + v ) / ( 1 + v_x^A ∙ v / c² )
v_y^B =   v_y^A       / ( 1 + v_x^A ∙ v / c² ) γ
v_z^B =   v_z^A       / ( 1 + v_x^A ∙ v / c² ) γ

We can not put v_x^B, v_y^B and v_z^B directly into the Newtonian momentum conservation law, because in Bob’s frame the form of the law of nature is different from that of the Alice’s frame, which means relativity is no longer preserved. The problem lies in the additional term ( 1 + v_x^A ∙ v / c² ), which breaks the invariance of the law of nature in different frames.

Relativistic Momentum

The problem described above was caused by the differentiation of time, which is not invariant in one frame compared to another frame. The differentiation of time changing a frame give you the additional factor.

dt_B = γ ( 1 + v_x^A ∙ v / c² ) dt_A

Try to fix that, we’d like to redefine momentum, replacing the differentiation of time with the differentiation of another quantity, which shall be invariant under the change of frame. There is a good candidate: invariant interval ds².

Proper Time

Proper time is defined as dτ = √(-ds²/c²). Let’s try to expand it:

dτ = √(-ds²/c²)
= √(- d(ct)² + dx²)
= dt √[1 - (1/c²)(dx²/dt²)]
= dt / γ

The result shows if we fixed dt by factor γ, we will get an invariant quantity dτ called proper time. To understand the physical meaning of the proper time. Let’s find out an observe whose time coincides with the proper time. That will be the observer whose dx² = 0, i.e. γ = 1. That observer, is the observer who is with the clock and moving together with the object, for the object we like to define momentum.

With the help of proper time, finally we are able to write down the relativistic momentum, which gives you consistent and invariant momentum conservation laws in a different frames.

P^→ = m dx^→/dτ = γ m dx^→/dt

Relativistic Force

Once we have defined relativistic momentum, we can directly define relativistic force.

F^→ = dP^→/dt = d(γmv^→)/dt

Here we are not using proper time, but we are using the time of an observer who is standing watching the object moving. Using physical time instead of proper time is convenient because when we are talking about force, we stand here, push something and see how much work I have done and how much momentum transfer there is.

Force is not only related to acceleration, but there is factor γ. Recall that γ = 1/√(1 - v²/c²), so when the speed v is approaching the speed of light c, γ is approaching infinite. That means if there is an object which originally is moving slower than the speed of light, then if we push it, it is impossible to be faster than light, because of the gamma factor. If the object is approaching the speed of light, you’ll need infinite force to accelerate it even a little bit, and eventually you’re unable to make this object exceed the speed of light. This preserves the causality that we have discussed, that subluminal motion of objects cannot be accelerated to be superluminal.

Relativistic Kinetic Energy

The definition of kinetic energy is the integration of force over space interval.

K = ∫^x₀ F dx
= ∫^x₀ d(γmv)/dt dx          # change limit
= ∫^v₀ d(γmv)v               # integration by parts
= ∫^v₀ d(γmv²) - ∫^v₀(γmv)dv
= γmv² + γmc² - γmv² - mc²
= (γ-1)mc²

Actually the relativistic kinetic energy could be the Newtonian kinetic energy, i.e. 1/2 mv², when speed v is very small. Using Taylor expanding of γ, we could get:

(γ-1)mc² = [(1 + 1/2 v²/c² + ...) - 1] mc² = 1/2 mv²

Kinetic energy is a process, it is talking about the status of the particle, not the history of the particle. As long as eventually the particle is accelerated to speed v, the kinetic energy is this form irrelevant of how you achieve this speed v, without caring about it was accelerated.

Mass is Not Conserved

It is a convention that the mass is a constant of boost (which means changing reference frames) with respect to different observers. However can mass be considered a conserved quantity? In other words, if the total mass of the initial state equals to the total mass of the final state?

( ∑ m_i )_initial ?= ( ∑ m_i )_final

Think about a particular scenario. Initially, two objects (each with mass m) are binding together with a spring. The final state is the spring is broken and two objects (still, each with mass m) are moving apart from each other with speed v, in the horizontal direction. The question is: “Is the total mass M in this problem is conserved or not, in special relativity?”

Let us consider a observer which is moving very slowly in the vertical direction, but objects’ speed v is very fast, in this case the γ factor is dominated by the motion in the horizontal direction.

Initial state momentum	`P = M v` There is no `γ`, because there is no motion in the horizontal direction, and motion in vertical direction is very slow.
Final state momentum	`P = 2 γ m v`

Because the momentum is conserved quantity, we could have M = 2 γ m (not M = 2 m). That means the initial elastic potential energy of the spring will contribute to the mass. Even if the mass of the spring is not important, the energy of the spring contribute to the total mass M, which makes the total mass of the initial state to be 2 γ m.

However the total mass of the final state is 2 m, so the mass is not a conserved quantity from initial state to the final state.

Rest Energy

Assume special limits:

the motion of the objects are extremely fast: v → c, γ → ∞.
the objects themselves are extremely light: m → 0.
γ m → some finite number.

With these limits, we can write down the energy conservation equation of the initial and final state.

Initial state energy (Rest energy only)	`E = M c²`
Final state energy (Kinetic energy only)	`K = γ m c² - m c²` `E = 2 K = 2 γ m c²`

From energy conservation we know that the final state energy has to be equal to the initial state energy, from which we could see M = 2 γ m again. The famous E = M c² is the relation between rest mass and rest energy.

Generally, the total energy E equals to rest energy plus kinetic energy:

E = M c² + (γ-1) M c²
= γ M c²

Rest energy is huge even for a small object. For example: a 10-grams object will have 10¹⁵ J energy.

Rest energy can also be released in relativity, for example, to the kinetic energy in the previous example above. In Newton’s mechanics, mass is conserved, then the energy from mass is not released, so energy is conserved as well. So rest energy in the initial state and final state is always the same. That’s why Newton’s mechanics didn’t realize there is such a huge rest energy.

Other examples include nuclear fusion or nuclear fission, can be considered as the rest energy, which is the energy of the atom can be released and to make power.

3-Vectors

In a vector, three dimensions (x, y, z) are not individual things, the three dimensions are tied up by operation known as rotation. Different observer A, B with different angles θ_A, θ_B look at the same vector v^→ will have different component (x_A, y_A, z_A) and (x_B, y_B, z_B).

However there are invariant quantities in rotation. One example is inner product of vectors , that is irrelevant of which angle you are looking at it.

v₁^→∙v₂^→ = x₁x₂ + y₁y₂ + z₁z₂ = |v₁| |v₂| cos(θ)

The inner product of a vector with itself is the square of its magnitude.

v^→∙v^→ = x² + y² + z²

4-Vectors

Recall invariant interval, which can be separated into the general product of two 4-vectors.

ds² = - d(ct)² + dx² + dy² + dz²
= -c² dt² + dv^→2 = dv ∙ dv

where dv (with underscore) is a 4-vector (c dt, dv^→), then we can define inner product of one 4-vector with another 4-vector, which is also invariant under Lorentz Transformation.

dv₁ ∙ dv₂ = -c² dt₁ dt₂ + dv₁^→ ∙ dv₂^→

Once we know the 4-vectors, we can immediately construct a lot of other quantities which are invariant under Lorentz transformation.

Momentum in 4-Vector

We can promote a 3-dimensional momentum into the form of four-vector. We already have the space dimension already and then we have to add a time dimension to it.

momentum in 3-dimension	`P^→ = m dx^→/dτ = γ m dx^→/dt = γ m v^→`
momentum in 4-vector	`P = (γ m c dt/dt, γ m v^→) = (γ m c , γ m v^→)` `= (E/c, P^→)`

The length (inner product) of P is:

P ∙ P = -(E/c)² + P^→2 = - γ² m² c² (1 - v²/c²) = - m² c²

The implication is indeed the length of p is an invarient quality. So this is why we prefer to use the convention where mass is a constant, it is not changing with velocity. Because in this way the mass is an invariant quantity of the length of momentum (a four vector).

By multiplying c² to the length of P, we could derive another useful equation:

E² = |P^→|² c² + m² c⁴

One limit is when the particle is at rest, E = m c². Another limit is when the mass m is vanishing, all the energy is from the kinetic energy, which corresponds to light and γ is infinite, and we get E = |P^→| c.

Relativistic Doppler Effect

When we have two four-vectors, we can construct invariance of themselves (the length) and also the invariance of one vector inner product-ed with another vector. A well known application is the relativistic Doppler Effect.

Suppose Alice is moving with 3-dimensional velocity v^→. Alice emits a beam of light E, where this beam of light and the motion of Alice has a relative angle θ. Bob is standing on the ground to observe the whole thing. With respect to Alice, the energy of the light is E_A and with respect to Bob, the energy of the light is E_B. What is the relation between E_A and E_B? By using 4-vectors, this problem can be solved without much effort.

First we use 4-vectors to write down the definition of the problem:

	4-vectors
Alice in Alice’s frame, who considers herself not moving.	`k_A = (m c, 0^→)`
Light in Alice’s frame	`P_A = (E_A / c, P_A^→)`
Alice in Bob’s frame, seen by Bob	k_B = (γ m c, γ m v^→)
Light in Bob’s frame, seen by Bob	`P_B = (E_B / c, P_B^→)`

Now the magic is the 4-vector inner product is invariant, is irrelevant to which observer you are talking to. In other words:

k_A ∙ P_A = k_B ∙ P_B
⟹ -m E_A = -γ m (E_B - v^→ ∙ P_B^→)
⟹ E_A = γ (E_B - v^→ ∙ P_B^→)
⟹ E_A = γ (E_B - v P_B cos(θ))
⟹ E_A = γ E_B (1 - v/c cos(θ))

Spacetime Metric

A metric literally means to measure something. Here a metric is to measure how an inner product is defined. This is a inner product of a 4-vector itself, formally, we can define a metric like this.

ds² = -c² dt² + dv^→2 = ∑³_μ=0 ∑³_ν=0 g_μν dx^μ dx^ν
where dx^μ = (c dt, dv^→)
g_μν = -1 0 0 0
       0 1 0 0
       0 0 1 0
       0 0 0 1

This tells you how to define the length of two vectors and actually in general relativity, matter curve space, where matter can change this g_μν into a nontrivial form. Metric is a trivial in special relativity, but in general relativity that will be the object to study.

Natural Units

Since space and time, they are not exactly the same thing but they are highly related, we can choose a unit where space and time looks even more similar. We can choose c = 1. If we still measure time by seconds, then we can measure space by the distance that light can travel per second. However natural units do not mean convenient units.

Another examples include: In Thermodynamics, energy and temperature are related by a Boltzmann’s constant. Energy and temperature are almost the same thing, closely-related in statistical situations. We can choose R_B = 1. In quantum mechanics, energy and frequency can be related by a Plank’s constant. We can choose h = 1. This natural unit is the most convenient unit system if we study fundamental physics, for example, quantum field theory.

My Certificate

For more on Special Relativity: Geometry, Momentum and Energy, please refer to the wonderful course here https://www.coursera.org/learn/understanding-modern-physics-1-relativity-and-cosmology

My #100 course certificate from Coursera

Related Quick Recap

Lorentz Transformation

I am Kesler Zhu, thank you for visiting my website. Check out more course reviews at https://KZHU.ai