The computation is a physical process, which is finite in time with fixed and distinguished set of states. It always consumes or transforms energy meanwhile keeps distinguishable states. Computations transform or process information.
Information is actually an interpretation of the particular system states. Two different systems with different states can actually present the same information. The point is to invent some conventions about how we would interpret these system states, i.e. how would we read information from them.
Information as Energy
The first mathematical notion of quantity of information was introduced in 1948 by Claude Shannon. The amount of information can be stored by a system with N states was defined by his famous formula:
I = - ∑ni=1 Pi logb(Pi)It is the sum over all states of the probabilities of each state Pi, multiplied by the b-based logarithm of this probability. The probabilities come from physics. Physicists are interested in much more general set of physical processes. But for computational processes, all these probabilities usually are equal to each other. i.e. equiprobable Pi = Pj = 1/n.
I = ∑ni=1 1/n logb(n) = logb(n)So, the amount of information stored by a system with n equiprobable states is the b-based logarithm of the number of states. The smallest amount information is called a bit: log2(2) = 1. According to the thought experiment of Leo Szilard in 1929, in order to assign a value, we have to dissipate some energy. The work done is A = kB ∙ T ∙ ln2. However negating a value (the NOT operation) does not need to dissipate any energy. The NOT operation did not do any work, it is reversible. Erasing operation will give the same amount of energy back. So the information in some sense equals to energy.
Characteristics of Computational Systems
There are a few important characteristics of computational systems:
- Information capacity
- Speed of switching between states
- Universality, the repertoire of a computer system.
For increasing the capacity and speed, over the decades, engineers try to make the base element as small as possible, from vacuum tubes, to transistors, to integrated circuits, to microprocessors, etc. Now computer device has reached the limit. At some point, we are not able to construct smaller transistors and the growth of our computing power will eventually stop. The new solution has to be as small as atom or even smaller, but at this scale we can not disregard the quantum effects.
For the analogous computing systems using continuous parameters, there are two main drawbacks. First, it is hard to implement the error correction. Second, the lack of universality, many functions can not be or hard to be realized. These drawbacks can be fixed by introducing digitization to computing systems. The digital systems usually have bigger and better universality (larger repertoire) than the analogous ones.
Computability
Computation transforms information, because it maps some input data to some output data, so does any function. Functions have a strict mathematical definition. A function can be computed if there is an algorithm for it. Algorithm is a deterministic Turing machine. For any function to be computable, it means there is a DTM which computes this function.
Function → Algorithm → DTMDTM is a very powerful model because it allows us to define the Universal Turing machine, which is a Turing machine accepting another Turing machine as its input and emulates its behavior. So this Universal Turing machine can do anything that any other DTM could do. There is no other deterministic computing devices if their repertoire are larger than that of Universal Turing machine.
Since any DTM is a finite tuple of finite sets and elements, it can be encoded as a finite string in some alphabet, say 1s and 0s. Any such string can be mapped to two natural numbers: 1) the numbers of leading zeros; 2) the number represented by this string in binary encoding. For example: if the string is 00011001, then the 2 numbers are 3 and 25 (0x19). The set of two numbers is countable, we only have a countable infinity of deterministic Turing machines. The set of all DTMs is countable.
However the cardinality of the set of functions, which map natural numbers to 1 bit, is continuum. It means that there are uncomputable functions, since the number of DTMs is less than infinity. Even more if we take a function from the (infinite) set randomly, the probability of the event we can compute is zero. We can compute almost nothing.
Not all of uncomputable functions are bizarre or useless. One example is the halting problem, in which a function H takes another DTM as input. Turing proved that this function H is uncomputable. It means that deterministic Turing machines can not analyze deterministic Turing machines.
Computational Complexity
It appears that those computable functions are not all the same. Some are easier to compute, some are harder. For example, assume a graph with some vertices and edges, consider two problems:
- Finding Euler’s path (which visits every edge exactly once).
- Finding Hamiltonian path (which visits every vertex exactly once).
The first problem is known to be easy. The second problem is believed to be hard.
There are actually plenty of parameters allowing us to estimate algorithms. A good choice is to use “time” or “number of steps” of a deterministic Turing machine needed to perform the computation.
Another example is addition of 2 n-bits integer numbers vs multiplication of them. The addition operation will require at most 2n elementary additions. The complexity (the number of steps) is O(n). However multiplication will require approximately n2 elementary operations, which means the complexity is O(n2). Actually any finite power tells us the problem is not so bad. Polynomial-time problems are still considered tractable.
All such problems form the class called P (for polynomial), in this class, problems can be solved in polynomial time. There is another interesting class of problem called NP (for non-deterministic polynomial), in which the problem can not be solved in polynomial time, but can be verified in polynomial time. It is believed that there are problems which belong to NP but do not belong to P, though we can not prove it, yet. One of such important problem is factoring problem.
In 1994, Peter Shor designed a quantum algorithm which solves the factoring problem in polynomial time. So now quantum computers can solve problems that are intractable for classical computers.
Quantum Computing
When we want to base our computer on something as small as a atom, we have to deal with the problem of quantum effects, as well as the problem that the system with several quantum elements is hard to model. In 1985, David Deutsch developed a mathematical model of universal quantum computer.
Quantum Effects
You probably have noticed that the light does not propagate in the same direction, the spot of light becomes wider as light travels further. Even for a directed radiation coming out of a laser, we still have this effect. The reason of this is the Heisenberg’s uncertainty principle, which tells us that we can not have a perfect measurement of both the momentum and coordinate of the particle. The double slits experiment is a good demonstration of this principle.
For the photons coming out of the laser, we perfectly know their wavelength and momentum; then we must have problems with their coordinates. We also know the distance (the x coordinate) from the photon emitter to the double-slit screen, then there must be problems with the coordinates y and z on the screen.
Question 1: Even though the photon was emitted one by one, but it looks like it behaves like there were two of them, i.e. two photons.
We have to consider some probability distribution of position of the photon, among all the possible paths. In the double-slits experiment, there is one upper slit, one lower slit, so there are 2 paths. Instead of one photon having one position at each point of time, we have to consider the probability distribution of its positions, this probability distribution is called wave function.
Question 2: Suppose we have already gotten a wave function, what will happen if we place a detector after one of the slits?
This will make the wave function of the photon to collapse. If we want to keep the wave function from collapsing, the system must be closed. There must be no interaction with some other systems. The placement of a detector is actually introducing some interaction, this will cause the wave function of photons to collapse.
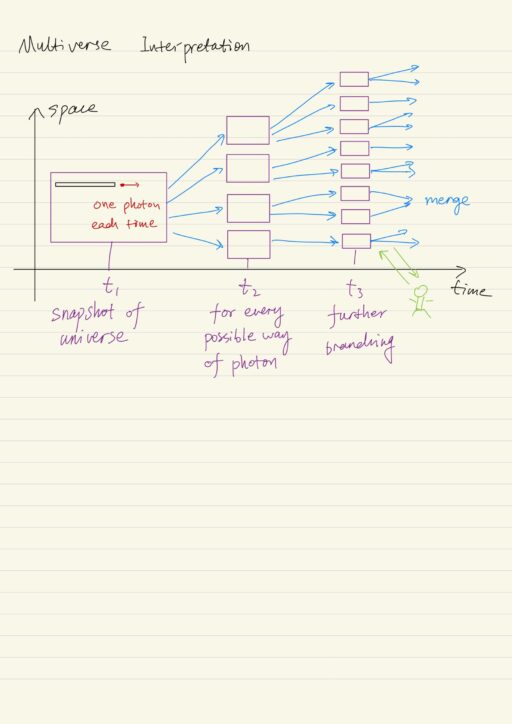
Multiverse Interpretation of Quantum Mechanics
Observation does not alter the wave function of the system observed, on the contrary, the observation alters the wave function of the observer. Actually the observation process is the process of recording information about the system into the state of their observer.
The question is where do these copies of observers exist and why they don’t see each other. In 1957, Huge Everett III suggested that, instead of believing that this split state of the observer is some kind of wave function, it is better to believe that these different copies of observer actually exist.
Imaging there is a coordinations, the horizon axis is time, the vertical axis is the space. The world could be seen as a snapshot in a point of time. And for every possible way, the snapshot will branch to many other snapshots. We as observers, at some time point, observe and have recorded information in ourselves, so our wave function splits. Then subjectively, we observe only one of branches.
This is what all quantum computation is about, first we build a highly isolated system, then introduce the branching on some parameter, after that, we somehow make the system to interfere and we want to read the result from this interference.
My Certificate
For more on Computation from Classical to Quantum, please refer to the wonderful course here https://www.coursera.org/learn/quantum-computing-algorithms
Related Quick Recap
I am Kesler Zhu, thank you for visiting my website. Check out more course reviews at https://KZHU.ai



