Computational Secrecy, Pseudo-randomness, and Proof of Security

Limitations of the One-Time Pad

The one-time pad encryption scheme achieves perfect secrecy, but nowadays it is not often used because of several limitations:

1. The key is as long as the message.
2. Only secure if each key is used to encrypt a single message.

Actually these limitations are not specific to the one-time pad scheme, they are inherent for any scheme achieving perfect secrecy.

---

---

Theorem: if a scheme (Gen, Enc, Dec) with message space M is perfectly secret, then the size of key space is at least the size of message space: |K| ≥ |M|. It means if we use some fixed length bit strings, the length of the key is at least the length of the message that can be encrypted.

The proof is simple:

1. Given a cipher text c, we could try to decrypt under every possible key in K. This gives a set {Deck(c)}k∈K of the size up to |K|.
2. If the size of the key space |K| is smaller than the size of the message space |M|, then |{Deck(c)}k∈K| ≤ |K| < |M|, i.e.: there are some messages that are not in the set.
3. These messages m could not possibly have been the messages that the parties encrypted and wanted to communicate with each other, i.e.: Pr[M = m | C = c] = 0 ≠ Pr[M = m]. The perfect secrecy does not hold.

We need to relax the definition of perfect secrecy, and obtain a definition which is still meaningful and useful in practice.

Computational Secrecy

Perfect secrecy	Absolutely no information about the plaintext is leaked, even to eavesdroppers with unlimited computational power.
Computational secrecy	Leak information with tiny probability to eavesdroppers with bounded computational resources.

If something occurs with probability 2^-60 per second, it is expected to occur once every 100 billion years. Consider brute-force search of key space, assume one key can be tested per clock cycle, then the attacker can search through about 2⁵⁷ keys per year on a typical desktop computer, or 2⁸⁰ keys per year on a supercomputer, or 2¹¹² keys on a supercomputer even since Big Bang. We don’t need to worry about attackers who can test 2²⁵⁶ keys, simply because there is no way such an attacker can possibly exist in our physical universe. In modern encryption schemes, the key space has at least 2¹²⁸ keys or more.

Perfect Indistinguishability

Let Π be an encryption scheme (Gen, Enc, Dec), and let A be an attacker. We define a randomized experiment called PrivKA,Π that depends on fixed A and fixed Π:

1. A (the attacker) gets any two messages m₀ and m₁ of its choice from the message space M.
2. We generate a key k using the key generation algorithm: k ← Gen
3. We select a message uniformly: b ← {0, 1}
4. We encrypt the message using the key: c ← Enck(mb)
5. We give the cipher text c to A.
6. A (the attacker) outputs b’, which is meant to represent A’s guess as to which of the two messages was encrypted.
7. In a given run of experiment, A succeeds if b’ = b. The experiment evaluates to 1.

It is easy for any attacker A to succeed with probability 1/2 (with some random guess). We will say that the encryption scheme Π is perfectly indistinguishable if there is no attacker A who can do better than 1/2.

Pr[ PrivKA,Π = 1] = 1/2

Π is perfectly indistinguishable if and only if it is perfectly secret. The definition of perfect indistinguishability is equivalent to that of perfect secrecy.

---

---

Relaxation of Perfect Indistinguishability

There are two possible ways to relax the perfect indistinguishability.

Concrete Version

Π is (t, ɛ)-indistinguishable if, for all attackers A, running in time at most t, it holds that:

Pr[ PrivKA,Π = 1] ≤ 1/2 + ɛ

Parameter t and ɛ are what we ultimately care about in the real world. So concrete security is very nice because it maps very cleanly on to things we ultimately care about in practice. However this approach does not really lead to a clean theory. The parameter t is very sensitive to the exact computational model. Furthermore, we would like to have some schemes where users are not bound to some particular choice of t and ɛ, but instead adjust the levels of security.

Security Parameter

Introduce the notion of a security parameter n ∈ Z⁺, which is fixed by honest parties at initialization, allowing them to tailor the security level, meanwhile it is known by adversaries. You may view n as denoting the length of key, it is used to build two functions:

1. The running times of honest parties as well as the adversaries.
2. The probability of success of the adversaries.

We are going to relax the notion of perfect indistinguishability as follows:

1. Restrict attention to “efficient attackers” running in time polynomial in n.
   • A function f: Z+ → Z+ is polynomial if there exists {ci} such that f(n) < ∑i ci ni for all n.
2. Security may fail with probability negligible in n.
   • A function f: Z+ → R+,0 is negligible if for every polynomial p there is an N such that f(n) < 1/p(n) for n > N.
   • A function is negligible if it is asymptotically smaller, than any inverse of polynomial function. For example: f(n) = poly(n) * 2^-cn, where c is some constant.

---

---

Probabilistic Polynomial Time

The notion of equating “efficient attackers” with “probabilisitic polynomial-time” is borrowed from Complexity Theory, where traditionally we define the notion of problems “that can be solved efficiently” as problems “that can be solved in polynomial time”.

poly * poly = poly	Polynomial-many calls to probabilistic polynomial time subroutine is polynomial time.
poly * negligible = negligible	Polynomial-many calls to subroutine that fails with negligible probability, fails with negligible probability overall.

We are going to require the Gen, Enc and Dec algorithms of a encryption scheme run in probabilistic polynomial time.

Gen	Takes as input 1n (the string of n consecutive 1s allows the Gen to run in time polynomial in n, because traditionally we allow algorithms to run in time polynomial in the length of their input). Outputs k (|k| > n).
Enc	Takes as input a key k and message m ∈ {0,1}* (binary strings of any length). Outputs cipher text c ← Enck(m).
Dec	Takes key k and cipher text c as input. Outputs a message m or an error.

Asymptotic Version

Fix some encryption scheme Π and some attacker A. We define a randomized experiment called PrivKA,Π(n) that depends on fixed A and fixed Π, and parameterized on the security parameter n:

1. Inform the attacker A about the value of the security parameter we are using, i.e. run A(1n). This also allows the attacker to run in time n.
2. The attacker picks any two messages m₀ and m₁ ∈ {0,1}* with equal length.
3. We generate a key k using the key generation algorithm: k ← Gen(1n)
4. We select a message uniformly: b ← {0, 1}
5. We encrypt the message using the key: c ← Enck(mb)
6. We give the cipher text c to A.
7. A (the attacker) outputs b’, which is meant to represent A’s guess as to which of the two messages was encrypted.
8. In a given run of experiment, A succeeds if b’ = b. The experiment evaluates to 1.

We say the scheme Π is indistinguishable if, for all probabilistic polynomial-time attackers A, there is a negligible function ε such that

Pr[ PrivKA,Π(n) = 1] ≤ 1/2 + ε(n)

The left hand side of the inequality Pr[ PrivKA,Π(n) = 1] is a function of n. On the right hand side, the ε(n) is a negligible quantity that decays to 0 faster than any inverse polynomial. We are allowing the possibility that attackers can succeed with probability slightly greater than 1/2, but that negligible part decays to zero faster than any inverse polynomial.

---

---

For example, consider a scheme Π where the best attack is brute-force search over the key space, and Gen(1ⁿ) generates a uniform n-bit key. So if the attacker A runs in time t(n), then:

Pr[ PrivKA,Π(n) = 1] ≤ 1/2 + t(n)*2(-n)

This scheme is indistinguishable because for any attacker running in time in polynomial time, t(n) must be polynomial, then t(n)*2(-n) is negligible. Different attackers will have different negligible functions that bound their advantage over 1/2.

Encryption and Plain Text Length

In practice, we want encryption schemes to encrypt arbitrary length messages, however encryption does not hide the plain text length. In general, we are willing to allow the attacker to learn the information of the length of the plain text. Since we are willing to give up that information, we need to take that into account in out definition.

Also be aware that leaking plain text length can often lead to problems, for example: encrypting ‘yes’ and ‘no’ answers to some questions, or encrypting compressed data, etc.

Pseudo-randomness

Pseudo-randomness serves as an important building block for computationally secret encryption scheme. “Randomness” is not a property of a string, but a property of a distribution over strings. A distribution on n-bit strings is a function D:

D: {0,1}n → [0,1] such that ∑x D(x) = 1

The uniform distribution on n-bit strings is the distribution U_n where Un(x) = 2(-n) for all x ∈ {0, 1}ⁿ.

“Pseudo-random” informally could be expressed as “cannot be distinguished from random (uniform)”. “Pseudo-randomness” is also a property of a distribution on strings.

Definition in the 1950s

Fix some distribution D on n-bit strings. x ← D means “picking a string according to D, and assigning that string to the variable x”. Historically, D was considered pseudo-random if it ‘passed a bunch of statistical tests’, for example:

1. Pr_x←D[1st bit of x is 1] = 1/2
2. Pr_x←D[parity of x is 1] = 1/2
3. Pr_x←D[A_i(x) = 1] = Pr_x←Un[A_i(x) = 1] for i = 1,…,n

The probability when x is sampled from distribution D, is close equal to the probability when x is sampled from the uniform distribution U.

But an attacker might come along with its own test, and if that test distinguishes x_U (the string x sampled from the uniform distribution) from x_D (a string x sampled from the distribution D), then D should not count as a pseudo-random distribution.

Distribution D is pseudo-random, if it passes every efficient statistical test.

Modern definition (concrete)

Let D be a distribution on n-bit strings, D is (t, ɛ)-pseudorandom if for all attackers A running in time t:

| Prx←D[A(x) = 1] - Prx←Un[A(x) = 1] | ≤ ε

---

---

Modern definition (asymptotic)

Denote security parameter by n (corresponding to the length of string), and some polynomial by p. Let D_n be a distribution over p(n)-bit strings. Now “pseudo-randomness” is a property of a sequence of distributions {D_n} = {D₁, D₂, …}.

The sequence {D_n} is pseudorandom if for every probabilistic polynomial time attacker A, there is a negligible function ɛ such that:

| Prx←Dn[A(x) = 1] - Prx←Up(n)[A(x) = 1] | ≤ ε(n)

So, on the left hand side of the inequality, for every value of the security parameter n, we can take two probabilities, take their difference and absolute value; on the right hand side, there is a function being negligible meaning asymptotically decaying to zero faster than any inverse polynomial function.

Pseudorandom Number Generators (PRGs or PRNGs)

A PRG is an efficient, deterministic algorithm that expands a short, uniform seed into a longer, pseudorandom output. Since sampling true randomness is very difficult, it is useful whenever you have a “small number” of true random bits, and want lots of “random-looking” bits.

Formally, let G be a deterministic, polynomial time and expanding algorithm. Expanding means that the output of G is longer than its input: |G(x)| = p(|x|) > |x|. G actually defines a sequence of distributions {D_n}. Each D_n is the distribution on strings of length p(n), defined by

1. choosing / sampling a uniform seed x ← Un.
2. applying G to that seed to obtain a string G(x) of length p(n).
3. outputting G(x).

Formally, we are defining a distribution D_n where the probability of any particular string y of length p(n) is equal to the probability with which G(x) = y when sampling x uniformly, which is exactly summation over all input x such that G(x) = y of the probability of x

PrDn[y] = PrUn[G(x)=y] = ∑x:G(x)=y PrUn[x]
= ∑x:G(x)=y 2(-n) # continue further manipulation
= |{x:G(x)=y}|/2n # number of input x such as G(x) = y divided by 2n

In the end, it is the number of x’s that map onto the string y, multiplied by 2^(-n), because we are sampling x from the uniform distribution on n-bit string, so the probability of any particular x in that set being chosen is 2^(-n).

G is a pseudorandom generator if {D_n} is pseudorandom. It means for all probabilistic polynomial time attacker A, there is a negligible function ε such that:

| Prx←Un[A( G(x) ) = 1] - Pry←Up(n)[A(y) = 1] | ≤ ε(n)

No efficient algorithm A can distinguish whether

1. it is given G(x) (the output of a pseudorandom generator when running on a uniform string x, the seed)
2. or it is given y (a completely uniform string).

So the pseudo random generator really is giving us something that looks random, it is producing for us strings of length p(n) that are indistinguishable for any efficient attacker from a uniform string of that length.

In practice

Unfortunately we don’t know if PRGs exist without resolving the question of whether P = NP. Never the less, we can:

1. Assume that certain concrete functions G are pseudorandom generators, and use them to build other cryptographic schemes.
2. Construct pseudorandom generators from weaker assumptions.

---

---

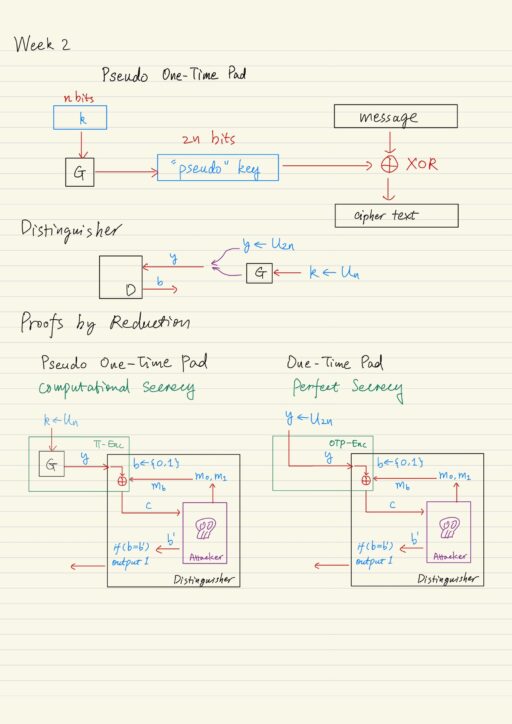
The Pseudo One-Time Pad

Recall that one of the limitations of one-time pad is that the key must be as long as the message. Now given the notion of computational secrecy, can we construct schemes which meet the notion of security at the same time overcome the previous limitations?

We can use pseudorandom generator directly to improve the efficiency of the one-time pad encryption scheme, at least in terms of the length of the key. So the parties can share a key now that is much shorter than the message we are encrypting.

Proofs of Pseudo One-Time Pad Encryption Scheme

We have defined “computational secrecy”, now our goal is to prove that the pseudo one-time pad meets that definition of “computational secrecy”. However we can not prove this statement unconditionally, because pseudo one-time pad was designed to depend on the pseudo random generator G. We can hope to prove the security of the pseudo one-time pad encryption scheme assuming that G is a pseudo random generator.

Let G be an efficient, deterministic function with |G(k)| = 2*|k|, which means its output is twice the length of its input. Suppose there is a distinguisher D, which could determine whether its input y was chosen uniformly at random, or whether y was output by running the pseudo random generator G on some uniform input.

Chosen uniformly at random	y ← U2n
Running the pseudo random generator	k ← Un y = G(k)

If G is a pseudo random generator that means, for any efficient distinguisher D, the probability that D outputs 1 in both cases is must be close.

Proof by Reduction

1. Assume G is a pseudo random generator.
2. Assume there is an efficient attacker A who ‘breaks’ the pseudo one-time pad scheme. By ‘break’, it means it violates the definition of computational security.
3. Use A as a subroutine to build an efficient distinguisher D that ‘breaks’ the pseudo randomness of G.
4. Now we have related the probability with which “D can break the pseudo randomness of G” to the probability with which “A can break the security of the pseudo one-time pad encryption scheme”.
5. But we know by assumption that G is pseudorandom, then there is no such distinguisher D can exist.
6. This implies that our initial assumption of A must have been false, and there could not exist such an A in the first place.

Analysis:

If A runs in polynomial time, so does D. Let μ(n) = Pr[PrivK_A,Π(n) = 1] = Pr[b=b’].

If input y of D is pseudo random, the view of A is exactly as in PrivKA,Π(n).	Prx←Un[ D( G(x) ) = 1 ] = μ(n)
If input y is uniform, A succeeds with probability exactly 1/2.	Pry←U2n[ D( y ) = 1 ] = 1/2

Since G is pseudo random, we will have:

μ(n) - 1/2 ≤ ε(n)
=> Pr[PrivKA,Π(n) = 1] ≤ 1/2 + ε(n)

This completes the proof. It shows that the pseudo one-time pad encryption scheme Π meets the notion of computational secrecy.

---

---

My Certificate

For more on Computational Secrecy, Pseudo-randomness, and Proof of Security, please refer to the wonderful course here https://www.coursera.org/learn/cryptography

My #90 course certificate from Coursera

---

Related Quick Recap

Introduction to Classical Cryptography

---

I am Kesler Zhu, thank you for visiting my website. Check out more course reviews at https://KZHU.ai