Transmission of Quantum Information

Unlike the classical bit, as we already know the quantum bit is able to stay in superposition state. When measuring a qubit in superposition state, one obtains every basis state with a certain probability. The probabilistic behavior of quantum objects has its effect on the logical operations.

---

---

No-cloning Theorem

Classical element FANOUT (bit-copying) could be realized using the reversible CNOT element. However it is impossible to create the quantum FANOUT element which would make a copy of a qubit in an arbitrary quantum state. This statement is known as the no-cloning theorem.

The CX element is the CNOT analog for quantum computations. Were it possible for us to copy the qubit, we would obtain the tensor product of the initial qubit and its copy, i.e.: (α|0⟩ + β|1⟩) ⨂ (α|0⟩ + β|1⟩), which would be a separable state of control qubit α|0⟩ + β|1⟩ and controllable qubit |0⟩ on the input. However in fact the CX element will bring our system to the state α|00⟩ + β|11⟩, which is actually an entangled state of the control qubit and controllable qubit. Thus the CX element does not lead us to the desired result.

It is easy to see that the obtained entangle state will be equal to the separable state, only when α or β equal to 0. This correspond to the situation where the quiet is already in the measuring instrument’s state |0⟩ or |1⟩, then a copy of a qubit could be created.

Theorem: in general it is impossible to create such a device that creates an identical copy of the qubit with the same quantum state. In other words, if one quantum system is in an arbitrary state |ψ⟩, and a second quantum system is in a certain state |ζ⟩, then there is NO unitary transform U such that

U: |ψ⟩ ⨂ |ζ⟩ → |ψ⟩ ⨂ |ψ⟩

This theorem prohibits the copying of a qubit, and it turns out to be crucial for the information security. I plays the main role in all protocols of quantum cryptography.

---

---

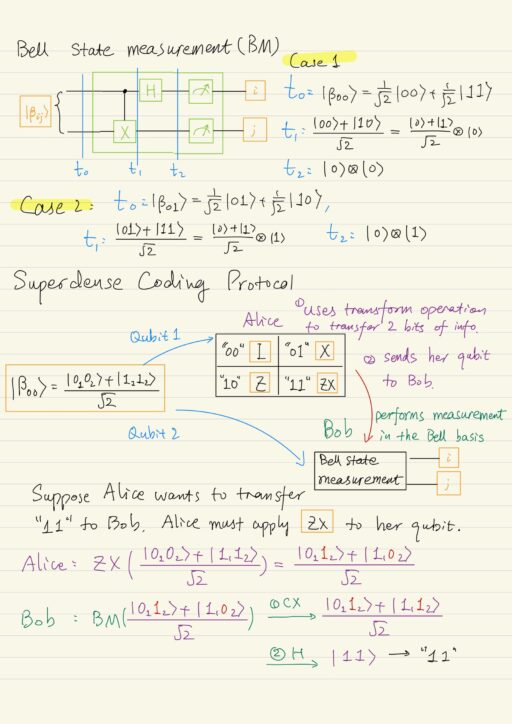
Superdense Coding Protocol

The classical information channel allows one to transfer classical bits of information, while the quantum one allows transferring qubits. Here the Bell state generation scheme and Bell state measurement scheme are defined.

Two people, say Alice and Bob, each of them has a qubit, these qubits were prepared in Bell state |β00⟩ at the beginning. If Alice’s qubit appears to be in the state |0⟩ after the measurement, then Bob’s qubit will also be in the state |0⟩ after the measurement. Alice’s and Bob’s qubit state shall be the same.

The two qubits in a Bell state act as a resource that Alice and Bob can use for the information transfer. Quantum entanglement between two qubits allows one to encode information using the qubit’s both value and relative phase. It allows one to transfer two classical bits of information using only a single qubit entangled with another qubit via the superdense coding protocol.

In this protocol, Alice transfers two classic bits of information to Bob by making certain logical operations on her qubit from the qubit pair and send the qubit to bob. Bob performs measurement of the qubit pair in the Bell basis and obtain the values of classical bits that Alice wanted to send.

In fact, Alice uses the quantum information channel, which allows one to transfer only qubits, to transfer classical information.

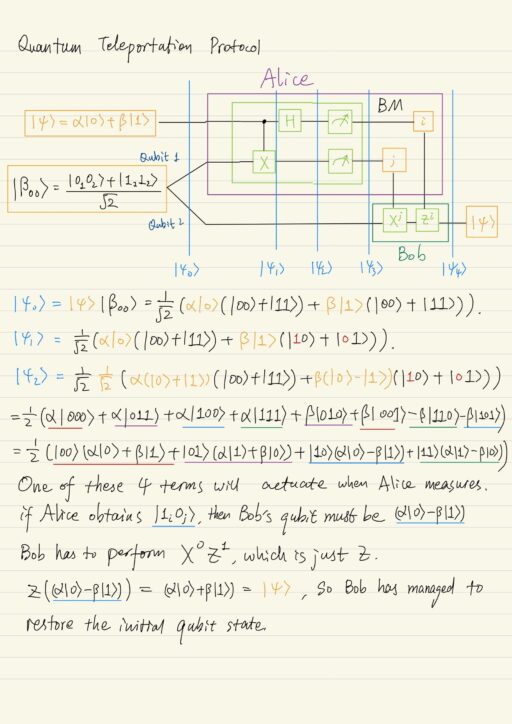
Quantum Teleportation

This protocol makes it possible to use a classical channel for transferring the quantum information. In other words, Alice can transfer the state of her qubit to Bob by using classical information channels. Everything that Alice needs for the state transfer is only one qubit from a qubit pair prepared from the Bell state, and a classical information channel. Bob has the second qubit.

We are actually talking about 3 qubits, Alice has 2 and Bob has 1:

Alice	Qubit 1: the qubit |ψ⟩ Alice wants to transfer to Bob. Qubit 2: in the Bell state with Bob’s qubit.
Bob	Qubit 3: in the Bell state with Alice’s qubit #2.

Alice’s task now is to use quantum teleportation protocol to transfer a known quantum state |ψ⟩ to Bob using the entangled pair of qubits via the classical information channel.

Quantum teleportation is a way to transfer a quantum state over long distances using a spatially separated entangled qubit pair and a classical communication channel. The quantum state of a physical system is destroyed at the transmission point during the measurement and recreated at the reception point on another physical system.

Quantum Teleportation does not allow one to transfer information faster than light, since data about the measurement is transferred through the classical channel. It is also impossible to make a copy of a physical system in the same quantum state, because the qubit’s state is destroyed at the transmission point. Moreover, one could use quantum teleportation to perform quantum logical operations.

Generation of Qubit Pair in Bell State

To date, quantum teleportation has been realized over pretty long distances, for example: between a low-altitude satellite and Earth (in 2017), the distance is about 1400km.

The process of spontaneous parametric down-conversion can be used to generate qubit pairs in Bell state. A strong laser pumping brings atoms of a type 2 nonlinear crystal into an excited state. The resonance pumping frequency is far off the resonance with the excited band, and the whole process is strongly non-resonant. As a result, the excited state appears to be unstable and decays quickly emitting a pair of photons.

The photons will propagate in certain directions and have certain energies. In optics, these photons are typically referred to as ones being radiated in certain modes (the signal and the idler). In accordance with the law of conservation of energy, the sum of energies of the signal and the idler must be equal to the energy of pumping photon (a generated parametrical process when ω_i = ω_s):

h ωp = h ωi + h ωs

---

---

In accordance with the law of momentum conservation, the total impulse also conserves and is often referred to as phase matching. The propagation directions of signal and idler photons are interconnected, and sum of the corresponding wave vectors of these photons must be equal to the wave vector of the pumping photon.

k→p = k→i + k→s

All the possible propagation directions of the photons can be described with a pair of cones, and wave vectors of the photons will lay on the surface of this two cones. Within the spontaneous decay, the signal and idler photons will have orthogonal polarizations with respect to each other. Moreover, these photons will be in an entangled quantum state. So if we measure the polarization of one of them, the polarization of the other one will be always orthogonal.

Assume that the photons have linear polarizations, so the quantum state |β11⟩, which can be used for quantum teleportation, is then a superposition of two terms, where → means horizontal polarization and ↑ means vertical polarization:

|β11⟩ = 1/√2 (|→s⟩|↑i⟩ - eiφ |↑s⟩|→i⟩)

Two-photon Interference: The Hong-Ou-Mondel Effect

We defined photons 1 and 2 as indistinguishable: the same polarization, the same frequency, and the same other characteristics. The only different thing is the initial direction. The state of two photons after passing the beam splitter is a superposition (where subscript 1 means the photon on the left, subscript 2 means the photon on the right, ← means goes to left, and → means goes to right):

|ψout⟩ = |←1←2⟩ + |→1←2⟩ - |←1→2⟩ - |→1→2⟩

The case where two photons go through the beam splitter without reflection |→1←2⟩ and the case where two photons bounce off |←1→2⟩ are completely indistinguishable from the point of quantum mechanics. These two terms remove each other and this is referred to as destructive interference. As a result, only the first and the fourth terms remain in the superposition, and the photons can only be received both by left or both by the right detector.

|ψout⟩ = 1/√2 (|←1←2⟩ - |→1→2⟩)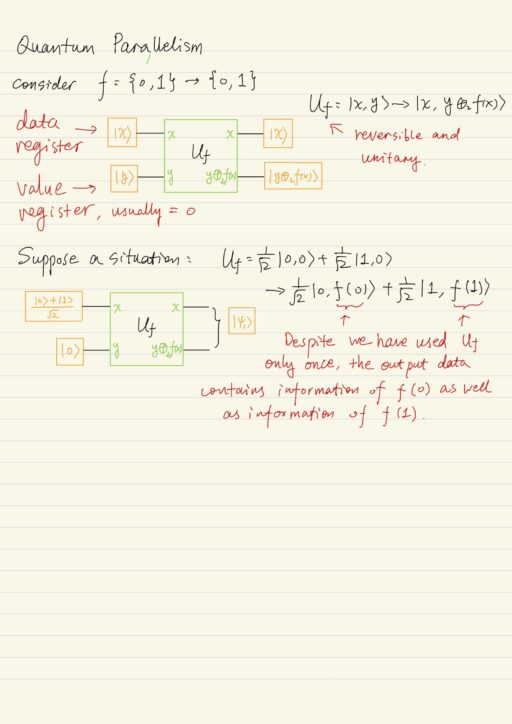

Quantum Parallelism

Quantum parallelism is a fundamental property of any quantum algorithm based on the quantum superposition principle. Quantum parallelism in quantum computational devices allows one to obtain several values of a certain function f(x) in points {x1, x2, ..., xn} simultaneously. It mean that only one unitary logical operation is needed:

Uf: {x1, x2, ..., xn} → {f(x1), f(x2), ..., f(xn)}

We took a superposition state as a data register at the input, and later we obtain a superposition state at the output. However, if we measure the superposition state, we will obtain only one of the values. This measurement makes quantum algorithm no better than classical algorithms. In order to benefit from the quantum computations, we must learn how to extract more information from the superposition state.

---

---

My Certificate

For more on Transmission of Quantum Information, please refer to the wonderful course here https://www.coursera.org/learn/physical-basis-quantum-computing

My #84 course certificate from Coursera

---

Related Quick Recap

Quantum vs. Classical Logical Operations

---

I am Kesler Zhu, thank you for visiting my website. Check out more course reviews at https://KZHU.ai