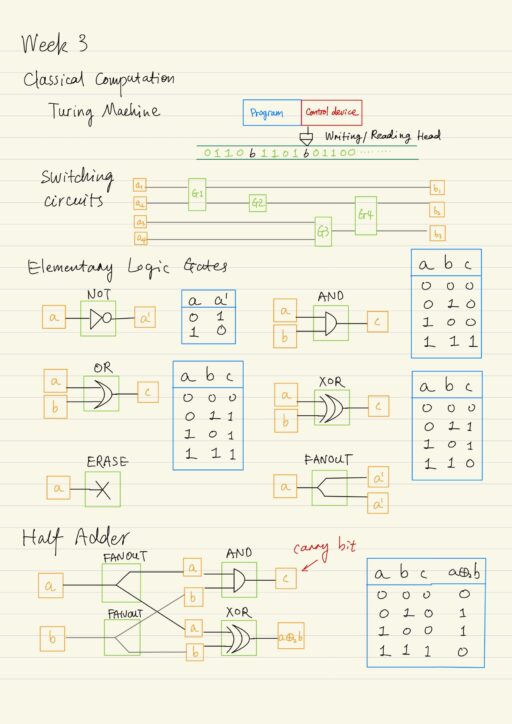
Nowadays, there are a large number of various computers. Despite the differences in physical implementations and the purposes of these devices, from the point of view on the computation theory, the operation principle of any of them can be described by Turing “machine”, which is formally called Church-Turing thesis. The main feature and advantage of Turing machine is its comparative simplicity.
In practice a equivalent circuit model, i.e. switching circuits, is often used as equivalent to the Turing machine. The circuit model is no longer infinite. This model is especially good and clear when we want to compare classical and quantum logical operations.
Elementary Logic Gates
| NOT (negation) | Change the value of a bit to the opposite.a' = a ⊕2 1 |
| CNOT (controllable negation) | Change the value of a bit to the opposite for a certain value of the control bit. |
| CCNOT (Toffoli) | Change the value of a bit to the opposite for a certain value of two control bits. |
| AND (conjunction) | Produce a logical multiplication.c = a ∙ b |
| OR (disjunction) | Return the largest value.c = a + b - a ∙ b |
| XOR (strict disjunction) | Is addition modulo two.c = a ⊕2 bc = max(a, b) - min(a, b) |
| ERASE | Delete a bit on which it acts from the computer memory. |
| FANOUT | Create a copy of a bit as its input. (Not possible in the case of quantum) |
To add numbers with several digits you need to apply a cascade circuit consisting of full adders and half adders.
Landauer Principle
Rolf Landauer showed when deleting or losing a bit of information, thermal energy is realized equal to ln2 times the product of the Boltzmann constant kb and temperature T of the physical system:
W = kb T ln2Moreover, such losses do not depend on the type of physical implementation. For classical computers, the Landauer Principle plays an important but not critical role. The heat emitted by a computer can be predicted by the Landauer Principle. However in quantum computing, the deterioration is somewhat different. Due to the smallness of the size of the elements themselves, any heating can lead to their deterioration. Qubit transformation must be unitary and reversible.
Irreversible Elements
For the AND, OR, XOR gates, there are situations when several different combinations of bits a and b can correspond to a value of bit c. All of them, as well as many others, are called irreversible. In addition, switching circuits (e.g.: full adders and half adders) complied using irreversible elements are also irreversible.
The fact is that, when performing logical operations using XOR, AND, OR, and other irreversible logical elements, we irrevocably loose some information about the state of the input bits a and b. This is the reason why we can not reverse the action. In physics, the destruction / demolition of information is a dissipative process. In such a process, some of the energy is converted into heat, thermal energy, or energy at controlled movement of the atoms and molecules that make up their physical system. This process is irreversible.
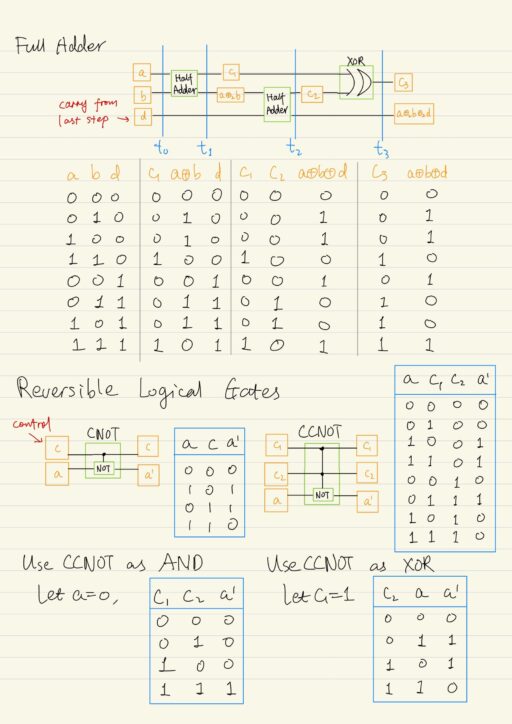
Reversible Elements
However NOT (negation), CNOT (controllable negation), CCNOT (Toffoli) operations are examples of reversible logical gate in classical computation. The truth table of CNOT element is the same to the truth table for XOR element. CNOT element can also be used to create copies as the FANOUT element. By using CCNOT element, you can get the elements AND, FANOUT, XOR and NOT. The effect of any reversible elements can be easily reversed if the same element is reapplied to the results obtained.
We could redesign the switching circuits for Half Adders and Full Adders using reversible elements CCNOT and CNOT.
Pauli Matrices
The Pauli matrices are three 2×2 matrices that form the basis for all 2×2 Hermitian matrices with zero trace. Together with the unit matrix, they form a basis for all Hermitian 2×2 matrices that are not only with zero trace. The Pauli matrices are widely used in physics to describe the spin 1/2, as well as in the quantum computation theory to describe single-qubit logical operations.
Properties
σ21 = σ22 = σ23 = I | The square of any Pauli matrix is identity matrix. |
σi = σ-1i = σ†i, i ∈ {1,2,3} | The inverse of any Pauli matrix is identical to itself. |
Tr(σi) = 0, i ∈ {1,2,3} | The trace of any Pauli matrix is zero. |
det(σi) = -1, i ∈ {1,2,3} | The determinant of any Pauli matrix is -1. |
The Pauli matrices are Hermitian, when taking Hermitian conjugation from any of the Pauli matrix, we gat the same Pauli matrix. They can be used to describe physical observables such as projectiles of the spin of an electron, proton, and other elementary particles.

Commutation
Pauli matrices do not commute with each other. εijk is Levi-Civita symbol.[σi, σj] = σiσj - σjσi = 2 i εijk σki, j, k ∈ {1,2,3} |
Anticommutator for distinct Pauli matrices is zero.σiσj i, j, k ∈ {1,2,3}; i ≠ j ≠ k |
The product of the two Pauli matrices could be expressed in terms of the Pauli matrices.σiσj = i εijk σki, j, k ∈ {1,2,3}; i ≠ j ≠ k |
In the production of Pauli matrices, we get either identity matrix (when i = j) or another Pauli matrix (when i ≠ j). The last property ensures that any Hermitian matrix A^ can be represented as a linear combination of Pauli matrices and the identity matrix.
A^ = c0 I + ∑3i=1 ci σiIn addition , any operator function of Pauli matrices can be represented as a linear combination of the Pauli matrices.
f({σi}3i=1) = a0 I + ∑3i=1 ai σi
The Circuit Model of Quantum Computing
As in the case of classical computation, a circuit model is used when developing practical applications and algorithms in quantum computing theory. The circuit model is also not infinite. A circuit is a network structure consisting of wires, through which qubits are transmitted to quantum logic elements (gates) that perform elementary operations on incoming qubits.
In accordance with the Landauer Principle, quantum logic elements (whose action can be described using a certain unitary quantum transformation) are initially made reversible. Otherwise the excess heat during the destruction of information could purely physically spoil them. So, if we have a set of qubits in the pure state at the inputs of quantum computer, then at the output of quantum computer, we also get a set of qubits in a pure state. Each quantum logical operation has its own unitary operator.
The choice of the basis is very important, because that will always associate the basis of some measuring device. Consider the qubit as a superposition of the eigenvectors of the Pauli matrix σ3, i.e.: |0⟩ and |1⟩, which is also called the computational basis. In some cases, we use eigenvectors of Pauli matrix σ1, which is |+⟩ and |-⟩, which is called Hadamard basis.
Single-Qubit Logic Elements
| X | Change the value of the qubit to the opposite. Similar to the classical element NOT. X|0⟩ = |1⟩Legend: X = σx = σ1 |
| Z | Perform a phase shift for |1⟩Z|0⟩ = |0⟩Recall, that an arbitrary state vector is defined up to the absolute phase ϕ. That is eiϕ where i is the imaginary unit, and φ is the absolute phase. If ϕ is equal to π, then eiϕ = -1.In the Hadamard basis, element Z plays the role of the NOT element: Z|+⟩ = |-⟩Legend: Z = σz = σ3 |
| Y | Change the value of a qubit to the opposite and perform a phase shift.Y(α |0⟩ + β |1⟩) = i(α |1⟩ - β |0⟩)Legend: Y = σY = σ2 = iXZ |
The logical operator X, Y, Z, acting on the state ψ are represented as rotations around the corresponding axes of the Bloch sphere. The logical element X rotate around the x-axis counterclockwise, with the angle φ = π. We will get similar situations for Y and Z.

| H | Hadamard element. Perform the transition from one basis to another. H|+⟩ = |0⟩, H|-⟩ = |1⟩H(α |0⟩ + β |1⟩) = α/√2 (|0⟩ + |1⟩) + β/√2 (|0⟩ - |1⟩) |
| T | Phase element. Act on the state of the computational basis as follows: T|0⟩ = |0⟩ |
A set of unitary elements is called universal for single-qubit elements, if any other single-qubit unitary element can be obtained through a quantum circuit build only on elements from this set. The sets of elements {H, T} and {I, X, Y, Z} are universal sets for single-qubit elements.
| M | Measurement element. Imply some measurement procedure that is the interaction of the quantum object with the classical microscopic device, whose basis contains macroscopically distinguishable states. As a result of measurements over a qubit, a real number is obtained, and the state of the qubit itself is destroyed. |
Controlled Logic Elements
In contrast to single-qubit logic elements acting on one qubit, now several qubits are entered on the inputs of controlled logic elements at the same time. As in the case of classical calculations, qubits are divided into two types: control qubit and target qubit. A logical operation on target quibits is determined by the state of the control qubits. If the control qubit is a superposition of states, then each term of the superposition must be considered separately.
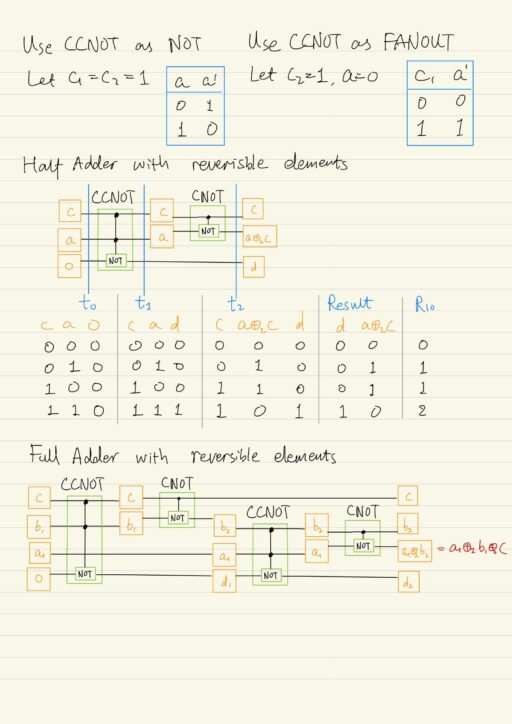
| CX | Controlled NOT element. Change the value of the target qubit |a⟩ to the opposite if the state of the control qubit |c⟩ = |1⟩, otherwise the state of qubit |a⟩ does not change.|c⟩ = α|0⟩ + β|1⟩CX transformation entangles the control and target qubits. |
| CCX | Double controlled NOT element. Change the value of the target qubit |a⟩ to the opposite if state of the control qubits |c1⟩ = |1⟩ and |c2⟩ = |1⟩, otherwise the state of qubit |a⟩ does not change. |
| CU | Change the value of a target qubit |a⟩ to U|a⟩ if the state of the control qubit |c⟩ = |1⟩, otherwise the state of qubit |a⟩ does not change. |
The set of elements {H, T, CX} is a universal set for any unitary elements, i.e.: a quantum computation circuit of arbitrary complexity can be constructed from these and only these elements.
My Certificate
For more on Quantum vs. Classical Logical Operations, please refer to the wonderful course here https://www.coursera.org/learn/physical-basis-quantum-computing
Related Quick Recap
I am Kesler Zhu, thank you for visiting my website. Check out more course reviews at https://KZHU.ai