Cosmology is the science of studying our universe. Being different from astronomy, which corresponds to studying some particular objects in our universe, for example, the black holes, neutron stars, etc. Cosmology is to study the universe as a whole object and study the universe itself:
- how this universe was born
- how it evolves
- what is the past
- what is the current state, and
- what is the future
An interesting observation is at night the sky is dark, and you could see star. A basic explanation is that the sun is on the other side of the earth at night.
Surface Brightness
However, why the sun (in the daytime) is brighter than the stars (at night)? There are two things to consider:
- The solid angle.
- The energy per unit solid angle.
Suppose the luminosity of the sun with radius r☉ is L☉, telescope has area A, then the telescope receives energy L☉ A / 4 π R2. The solid angle occupied by the sun is: π r☉2 / 4 π R2. So the power received by our telescope per solid angle is:
A L☉ / π r☉2which means it is defined by two things: the area of telescope A and the surface brightness of the sun ∑☉ = L☉ / π r☉2 = 5 × 10-3 Watt m-2 arcsec-2 . It has nothing to do with R, i.e. the distance between telescope and the sun. The sun looks brighter than a star because it spans a greater solid angle to us, however the energy per solid angle that we receive from the sun and that from the star are the same.
The surface brightness of the night sky is 5 × 10-17 Watt m-2 arcsec-2, the difference to that of the sun is about 10-14.
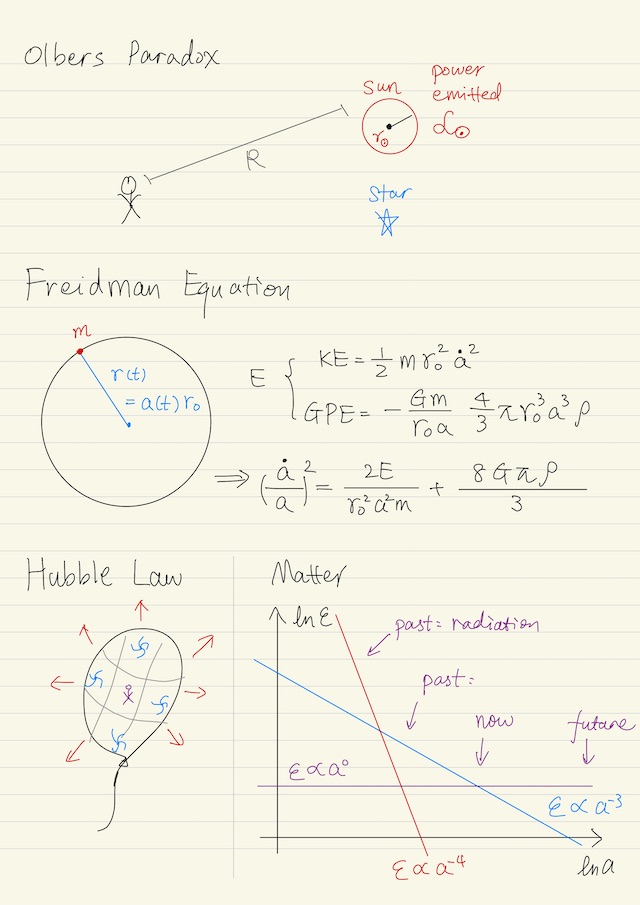
Olbers Paradox
If the universe is infinite, then for every solid angle, you can look into infinitely distant away, and you will encounter star finally. Since the brightness of stars equal to that of the sun, and you can encounter stars everywhere, adding all the brightness together, our night sky shall be as bright as the sun, like we are in the daytime. This problem is known as the Olbers paradox.
To solve the Olbers paradox, we could naively assume that the universe is finite with the size of the universe RU. If you look outwards (through an imaginary cylinder with radius equal to the sun’s radius r☉) there is a probability P that you’ll encounter a star:
P = n RU π r☉2 = 10-14where n is the density of stars and RU π r☉2 is the volume of the cylinder. Actually this probability P equals the ratio between the surface brightness of the night and the surface brightness of the sun, which is 10-14, like we talked above.
The density of stars n = 109 Mpc-3 (from Ryden 2017), where Mpc is a unit equals to 3 × 1022 meters or 3 × 106 light years. So the size of the universe RU is:
RU = 10-14 / (n RU π r☉2)
= 10-14 / (109 Mpc-3)(10-27 Mpc2)
= 104 Mpc
= 1010 light yearsHowever, are we really living in the center of the universe? No, assuming we are the center of the universe violates Copernican’s heliocentrism. And how do we solve this problem? Recall that light travels at finite speed, when we are looking into deep distance in the universe, we are also looking back in time.
Think about the star that we see in our universe. The starlight comes to us and that takes a long time. And that means, by the time we see the star, actually, that was the past of the star. If we see further and further, that corresponds to a earlier and earlier time of the universe.
If our universe has a finite radius, then our universe has a birth time and finite age. Any star beyond the birth (the boundary) of our universe can not be seen.
Observable Universe
Now, we arrive at the concept of the observable universe. The universe could be infinite, or finite, we don’t know, but we know there is a size of the observable universe, which is the age of the universe multiplying the speed of light.
Age of universe * Light speed = 1010 light yearsSo the age of the universe is roughly 1010 years. Our universe is not something exists forever, and it is in evolution.
Cosmological Principle
The most incomprehensible thing about the world is that it is comprehensible.
Einstein
Without being able to understand a lot of other details in physics, chemistry, biology, etc, we are able to understand a large part of our universe. The assumptions that we are going to make is known as the cosmological principle, which can date back to Newton and then was made sharper by Einstein.
The principle says: on large scales (from 100 Mpc to RU), our universe is approximately homogeneous and isotropic. (For small enough scale, this is not true.)
| Homogeneous | everywhere the physical condition is the same |
| Isotropic | every direction the physical condition is the same |
Homogeneous does not imply isotropy, for example, a constant electric field is homogeneous but not isotropic.
Cosmological principle tells us the state of the universe. If we’d like to study evolution of the universe from an initial state, we need some equations of motion, i.e. the dynamics. The most ideal, state of art dynamics is Einstein’s general relativity. The best combination will be the cosmological principle plus Einstein’s general relativity to study the dynamics of our universe.
However, Newtonian mechanics can also be used to solve the problem of cosmology if we consider them with special care. When there are paradoxes which cannot be explained by Newtonian mechanics, we still have to rely on general relativity.
Friedmann Equation
How to study the dynamics of the universe in Newton’s mechanics. Applying the cosmological principle, let us assume we have a universe filled with dust mater everywhere, uniformly homogeneously and isotropically. The matter is pressure-less, i.e. the density ρ is much greater than the pressure p, so the pressure can be ignored, p = 0.
First of all, we assume there is a center, consider the dynamics of the object (a matter element) away from the center with distance r(t), which is a function of time. For simplicity we parameterize r(t) as the scale factor a(t) multiplied by a constant r0, i.e. r(t) = a(t) * r0. Now we can study how this matter element moves.
First of all, we notice that if we divide the universe up to shells and shells of matter, the outer shells compared to this mass element wouldn’t be contributing to the motion of this element. So we don’t have to consider the shells outside and they are canceling, this is standard results from general physics. We only need to study the matter inside the shell how that is governing the equation of motion for this matter element on the shell.
The kinetic energy of this mass element is:
KE = 1/2 m v2 = 1/2 m (r0 a')2The gravitational potential energy of this mass element is, where ρ is the density of matter:
GPE = -G m M / r = -G m (4/3 π (r0 a)3 ρ) / (r0 a)Putting these two energy together, we get the total energy of the system E = KE + GPE, which can be reformed to this equation below, which is the well known Friedmann equation:
(a'/a)2 = 8/3 π G ρ + 2 E / m r02 a2 this equation at least we have two solutions: a’ > 0 means universe is expanding, a’ < 0 means universe is contracting. Hubble discovered that our universe is indeed expanding, so a' > 0 would be the correct choice. Historically, a’ = 0 was the first model that Einstein studied. A very small fluctuation can collapse the whole state of the Einstein static universe. So, a’ = 0 rarely happens, we do not consider this case.
Moreover, in our universe, E is very close to zero. The early universe inflation provides you a natural explanation of why this E = 0. The Friedmann equation in a flat universe now is:
(a'/a)2 = 8/3 π G ρThe expansion of the universe is governed by the density of matter ρ. If ρ is larger, the expansion speed of our universe is larger. “Matter tells space how to curve”, particularly in the context of cosmology, matter tells universe to expand. More matter, faster expansion.
Hubble-Leimaitre Law
Expansion is a key concept in modern cosmology. It can be thought of in two ways: general relativity (space is emerging) or Newtonian mechanics (objects are moving away from us). They are consistent as long as you think about small distances, but when it comes to the large distances as large as the observable universe, you had better to adopt the way of general relativity.
The way in general relativity is the modern view of the expansion of our universe. Let us imagine we live on the surface of the balloon, like ants. If we pump air into the balloon and the balloon becomes larger and larger, and the ants will feel that the space under its feet has expanded, and this expansion is very similar to the expansion of our universe.
The concept of expansion is that every neighbor point is moving away. For very closed points, the expansion will appear to be small and slow and for points far away to each other the expansion will be big and faster, because the expansion is proportional to the distance.
Measuring Expansion
Given the best possible telescope and the best observation conditions, you might want to measure the expansion of the universe by measuring the velocity r'(t) = a'(t) r0 as well as the distance r(t) = a(t) r0 of galaxies.
| How to measure | Method |
| distance r(t) | Assume galaxies are of the same order of luminosity. Compare original brightness and apparent brightness of a galaxy. |
| velocity r'(t) | Use atom spectrum (atom prefers to emit certain frequency of light). When an atom on a galaxy is moving away from us, then there is a Doppler effect. Measure the Doppler effect. |
We would like to investigate the relation between the speed and the distance.
r' = H r
⟹ H = r' / r
⟹ H = a'(t) / a(t)This is how to relate the Hubble parameter to our expansion. Hubble parameter squared is the Friedmann equation. Nowadays the Hubble parameter is about 70 km / s / Mpc.
Continuity Equation
Previously, we know that “Matter tells space how to curve”, in the context of cosmology, matter tells the universe how to expand. However this is not the whole story, matter has to move, following the expansion of the universe.
Think about the mass element and how it expands following the expansion of our universe. The key to this question is energy conservation dE = -p dV, i.e. the change of energy equals to the minus pressure multiplied by the change of volume. This is actually part of the first law of thermodynamics. The other term dS (the change of entropy) vanished, because the expansion of the universe can be considered as adiabatic, there is no change of entropy.
Assume the mass element is small enough so we don’t have to think about the gravitational effect, at the same time the mass element is large enough that the motion inside this element can be considered totally and statistically. Further assume the pressure exists, so p ≠ 0. Moreover, the energy density ε = ρ c2, where ρ is the mass density and c is the speed of light.
Transform the energy conservation using scale factor a:
dE = -p dV
⟹ d(ε a3) + p d(a3) = 0
⟹ dε/dt a3 + 3 ε a2 da/dt + 3 p a2 da/dt = 0
⟹ dε + 3 ε da / a + 3 p da / a = 0
⟹ ε' + 3 a'/a (ε + p) = 0 This equation is called continuity equation. This is how the expansion of universe tells matter how to move (dilute). Dilute means the energy density becomes smaller. This equation, plus the Friedmann equation tells us the evolution of our universe.
Matter
Because different matter can have different possibility of pressure, and then they evolve differently in our universe. There are only 5% matter of our universe that we currently understand well:
- Light 0.005%
- Starts 0.5%
- Free Helium and Hydrogen 4%
Remaining are the matter we don’t understand:
- Dark matter ~25%
- A form of matter which is extremely non-relativistic.
- There is vanishing pressure.
- We only study the energy density.
- Dark energy ~70%
- We don’t know what they are.
- They are a constant component of energy density.
We better off classify matter with their equation of state. i.e. pressure p as a function of energy density ε. A simple class of equation of state is p = w ε, where w is a constant and known as the index of the equation of state. If w is a constant, the continuity equation can be solved very easily.
ε' + 3 a'/a (ε + p) = 0
⟹ ε' + 3 a'/a (ε + w ε) = 0
⟹ ε' + 3 a'/a ε (1 + w) = 0
⟹ ε'/ε = -3 a'/a (1 + w)
NOTE: d(ln(x))/dx = 1/x
⟹ d(ln(ε)) = -3 d(ln(a)) (1 + w)
NOTE: up to integration constant
⟹ ε / ε0 = (a / a0)-3(1 + w)
⟹ ε = ε0 (a / a0)-3(1 + w)this is what we are looking for, the energy density ε evolves as the expansion of the universe. Now let’s look into details what matters are there in our universe and what’s the corresponding equation.
Non-relativistic matterp = 0ε ∝ a-3 | The energy density ε is dominated by its rest energy. Kinetic energy (compared to rest energy) is small. Energy is constant, there is no pressure. No work done by expansion, so energy density just dilutes directly as a function of scale factor a. |
(Extreme) relativistic matterp = 1/3 εε ∝ a-4 | There is no rest energy. All energy is in the form of kinetic energy. |
Dark energyε is constantε ∝ a0 | w = -1 |
This is what happens in our universe that divide our universe into a few stages:
| Past | Extremely relativistic matter (radiation) dominated our universe. |
| Then | Non-relativistic matter dominated our universe. |
| Current | Dark energy starts to dominate our universe |
| Future | If the dark energy is indeed the cosmological constant, it’s not decaying and not converting to other types of matter, it will all become more and more dominant in our universe. The other components are diluted away by the expansion of the universe. The dark energy is not diluted away. |
My Certificate
For more on Cosmology, please refer to the wonderful course here https://www.coursera.org/learn/understanding-modern-physics-1-relativity-and-cosmology
Related Quick Recap
I am Kesler Zhu, thank you for visiting my website. Check out more course reviews at https://KZHU.ai