Previously, in special relativity, we have found that the concepts of space and time are relative. When you are moving, you will find space and time are different compared to others. However, when you are not moving, gravity will also bring us new understanding about space and time. The Earth gravity is so weak that these effects are at the order of magnitude of no more than 10-8.
100 years ago, Einstein realized that Newton’s gravity is not consistent with his theory of special relativity. Einstein has to generalize his theory of special relativity to further include gravity. This is the starting point of general relativity.
Gravity is Related to Inertia
Newton claimed that there are two different kinds of mass:
Inertial massmI = F / a | How does the matter response to the change its status of motion? |
Gravitational massmG = F / g | How does the matter response to the gravity? |
Gravity is special because mI is equal to (or at least proportional to) mG. Gravity is special compared to other kinds of forces, for example, electric force, magnetic force, strong force, weak force, etc.
In 1907, Einstein stated in his ‘happiest thought’ that “If a person falls freely, he will not feel his own weight”. He proposed a way to “solve” the problem of why mI = mG, and explain why gravity is so special compared to other forces.
We … assume the complete physical equivalence of a (uniform) gravitational field and a corresponding acceleration…
Einstein
He has assumed that there are two systems:
- System A: a person in a box which is accelerating but without gravity
- System B: a person in a box which is not accelerating, but there is uniform gravity.
In this sense, without looking outside the box, the people inside the boxes won’t find out the difference between System A and System B. This is what he means by complete physical equivalence. So actually Einstein, by introducing assumption, “solved” the problem of why mI = mG, and explain why gravity is so special compared to other forces.
However assumption is only the starting point. To really solve the problems, you have to construct a theory out of the assumption. That was exactly what Einstein has achieved, that he has found that the most fundamental thing to construct his theory, is the equivalence principle, i.e. the equivalence between acceleration and uniform gravity.
Then in some sense, we could consider that the uniform gravity does not exist, because at least the uniform gravity can be cancelled by an acceleration, since gravity is equivalent to acceleration. Then there is no contradiction between Newton’s gravity with special relativity because there is no gravity.
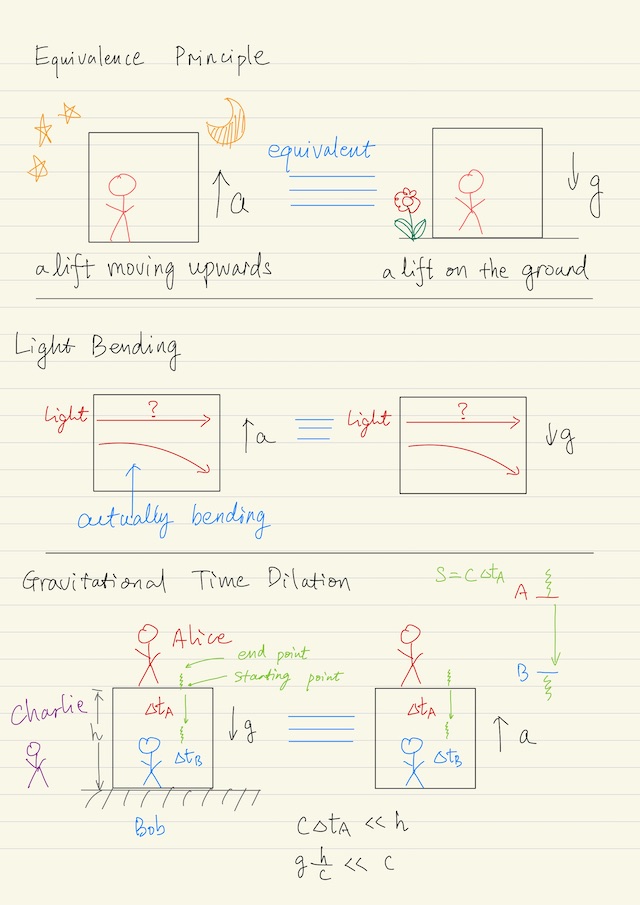
Light Bending
Will the gravity change the direction in which a beam of light emit? Newton’s gravity did not define this problem well, because it doesn’t tell about electromagnetic waves. However this problem can be solved using the framework of equivalent principle, by mapping a question of gravity into a question of acceleration.
Suppose there is a lift, a beam of light emits though the lift. If there is no gravity at all, but the lift is accelerating upwards. If you don’t look outside the lift, you won’t find a difference. The light bending happens in the lift, seen by an observer in the lift. So equivalence principle immediately tells you that light will bend in a uniform gravitational field.
Gravitational Time Dilation
The concept of time in general relativity can be discussed in the following situation. There is a lift of height h, Alice is standing on top of the lift, Bob is standing in the lift. There is gravity g. A beam of light was emitted, downward:
- Time point 1: first the starting point of the beam leaves Alice,
- Time point 2: then the end point of the beam leaves Alice.
- Time point 3: next the starting point of the beam reaches Bob.
- Time point 4: finally the end point of the beam reaches Bob.
The duration of light with respect to Alice is ∆tA = Time point 2 - Time point 1. Now the question is, with respect to Bob, in the gravitational field, what would Bob see about the duration of light ∆tB = Time point 4 - Time point 3?
How to calculate the time relativity of a gravitational field? This looks difficult because we haven’t learned the advanced theory of gravitational field. However we have already learned the equivalence principle and we can map this to a much simple case, in which the light is traveling in free space without gravity, but it is accelerating in the opposite direction.
One technical assumption must be made: the length of light beam is much smaller than the height of the lift, i.e. s = c ∆tA << h. So we don’t have to consider the speed difference of the lift, when the beginning point and end point of the light beam leave Alice and reach Bob.
Another technical assumption is v = g h / c << c, where h / c is the duration that the beam reaches the ground, and v = g h / c is the speed that Bob has built up when the light beam reaches Bob. So we don’t have to worry much about the special relativity effects. We could just imaging a third observer Charlie, who is observing the whole thing, we don’t have to worry too much about the time difference between Charlie and Bob, which is much smaller than the effect that we are considering.
Now the key point is: some time has elapsed since the beam of light leaves Alice and reaches Bob, and there is acceleration, as a result Bob has built up a speed when this beam of light reaches Bob. From the perspective of Charlie, the beam of light and Bob together consumed the length s, which is the length of the beam of light. So we have:
s = c ∆tA = (c + v) ∆tB
⟹ ∆tA = (1 + g h / c2) ∆tB
(where g h means gravitational potential difference)
⟹ ∆tA = (1 + (ϕA - ϕB) / c2) ∆tBAnd if we talk about age, Alice is growing old faster compared to Bob.
Schwarzschild Metric
We could use gravitational time dilation above to help us understand the gravitational field produced by a star. Suppose a situation where Alice is standing on a star with radius r and mass M. Bob is at very far away, essentially infinity from Alice. Now we have ϕB = 0, and ϕA = -G M / r and
∆tA = (1 - G M / r c2) ∆tBConsidering Alice is not moving, i.e. dx→ = 0, recall that proper time is defined as dτ = √(-ds2/c2). We could use the proper time that Alice observed to get this equation, which does not include d(x→)2 because Alice is not moving:
ds2 = -c2 dτ2 = -c2 dt2A
= -c2 (1 - G M / r c2)2 dt2B
(use Taylor expansion)
= -c2 (1 - 2 G M / r c2) dt2B
(there is no term dx→2 because Alice is not moving)The term (1 - 2 G M / r c2) applies to all the possible values. This is a consequence of solving the master equation of general relativity, i.e. Einstein equation.
For a moving observer, dx→ ≠ 0, the invariant interval is (using spherical coordinates instead of Cartesian coordinates):
ds2 = -c2 (1 - rs / r) dt2 <-- time change
+ (1 - rs / r)-1 dr2 <-- space change
+ r2 (dθ2 + sin2θ dϕ2) <-- space change
where rs = 2 G M / c2This invariant interval is known as Schwarszchild Metric. In the example of our earth, we human being are actually moving extremely slowly compared to the speed of light, the time dt2 term is the main reason why we feel earth gravity. In order to test the space term (dr2, dθ2, and dϕ2), we could use light. And we expect to see light bending in gravitational field.
However the earth is not heavy enough, and we as observers are too close to observe. Then the sun is a good candidate. Einstein predicted the light bending angle is 1.74 arc-seconds, which is later confirmed by Eddington. The light bending is the first observed prediction for general relativity.
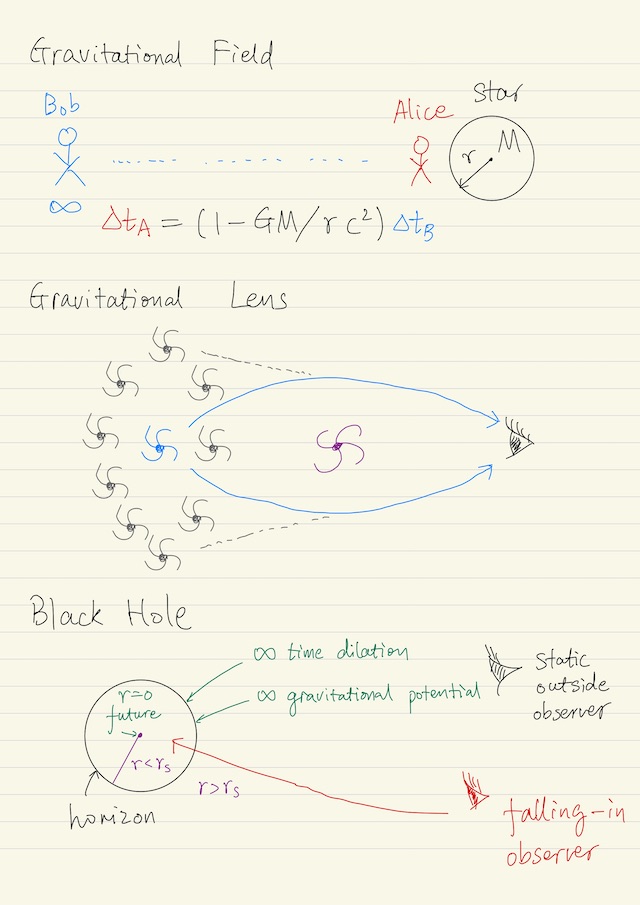
Gravitational Lens
Consider a situation that 2 galaxies and 1 observer are positioned on one same line. The light from the far galaxy will be bent by the near galaxy before traveling to observers eyes. If we have these perfectly aligned, we can observe a ring and this is predicted by Einstein. This is an important way to do astrophysical and also cosmological measurements. In our universe there is dark matter, which takes more energy (compared to observable matter) and does not emit light. So we have to rely on gravitational methods so far to see dark matter.
| Type | Effect |
| Strong Lensing | Long arcs |
| Weak Lensing | Shear |
| Micro Lensing | Brightness |
Black Holes
Recall the Schwarzschild Metric:
ds2 = -c2 (1 - rs / r) dt2 ...
where rs = 2 G M / c2when r is approaching rs (when getting closer to an extremely dense object), there are 2 ways to understand it:
- Infinite time dilation. Any finite interval
∆twill be approaching infinity time dilation for any far away observer. - Infinite gravitational potential. If we emit a beam of light, that beam of light will be infinitely red shifted. Each period of the light oscillation, will be considered to be extremely long at far away observer. That can be considered as the light loses all its energy, due to a infinitely deep gravitational potential.
Holographic Duality
An outside observer sees a two-dimensional surface which is termination of time, and gravitational potential is the same on any point of the surface. The outside observer will see you approach to this boundary, but they will never see you cross this boundary (known as event horizon). That means this dense object appears black. This is the reason why this dense object is called black hole, its surface is called black hole horizon.
However a falling-in observer inside the black hole will see there are three dimensions. The outside observers and falling-in observers see consistent, but apparently different description of the same black hole, and that is known as holographic duality: a two-dimensional theory without gravity (outside observers) is dual to a three dimensional theory with gravity (falling-in observers).
Journey of Falling In
Recall that when ds2 < 0 corresponds to a time-like interval, and ds2 > 0 corresponds to a space-like interval.
| When outside black hole r > rs | ds2 = -c2 (1 - rs / r) dt2 + (1 - rs / r)-1 dr2 + r2Ω2Because dt2 < 0, it is time-like.dr2 > 0, it is space-like. |
| When at the horizon r = rs | Extreme time dilation. Extreme gravitational potential. |
| When inside black hole r < rs | ds2 = c2 (rs / r - 1) dt2 - (rs / r - 1)-1 dr2 + r2Ω2Because ds2 > 0, it is space-like.dr2 < 0, it is time-like. |
The value r is reducing when the observer is falling in. When outside the black hole, r is a space direction, you can choose go anywhere. However when inside the black hole, r is a time direction, you can go forward in time only. r = 0 is somewhere in your future.
r = 0 point corresponds to space and time is curved so strongly that we cannot even trust general relativity.
Hawking Radiation
Black hole has infinitely deep gravitational potential, as a result, it is the most spherical objects in our universe if it is not rotating, and if it is rotating, it will become a different still perfect shape. Three parameter can characterize a classical black hole:
| M | Mass, how large it is, which is the size of Schwarzschild radius rs. |
| J | Rotation, which gives the black hole angular momentum. |
| Q | Charge. |
This really makes black hole look like a fundamental particle. However this is contradiction, for example black hole can decrease entropy which is in contradiction with the second law of thermodynamics. Quantum mechanics can help us understand black hole better.
Quantum mechanics tells us that the vacuum is not empty. The vacuum can spontaneously create pairs of particles and anti-particles, and one of the particle has positive energy, the other particle has negative energy. When this pair of positive and negative energy particles are spontaneously created, the state is unstable, due to quantum fluctuation.
If there is a pair of particle produced by quantum fluctuation and then the negative energy particle has fallen into the black hole. In this case, the positive energy particle can become a real particle and escape to infinity. In other words, the black hole is actually radiating in the quantum mechanical sense. This radiation is known as Hawking radiation.
Hawking radiation resolves the paradoxical entropy decrease problem in classical general relativity through the first law of thermodynamics.
dE = T dS + ...If we look at the quantum mechanical level, the black hole is actually full of entropy in it. In classical way we don’t see it, so that doesn’t contradict with the second law of thermodynamics at all.
Unfortunately we are not able to see Hawking radiation in any technology in the foreseeable future. Because the Hawking radiation is a quantum effect and the power of Hawking radiation is extremely small for solar mass black hole or larger black holes.
In practice, the black hole is not living in vacuum, it is not black, it is actually the brightest object in our universe. There is an accretion disk around the black hole which has matter which are to fall into the black hole but not yet falling into the black hole. Particles collide in this disk, a considerably fraction of the energy of the particles emitted in the form of light, say X-ray, because of the collision.
| Classically in vacuum | Black hole is a black object. |
| Consider quantum fluctuations | Black hole is not black because of the Hawking radiation, in order to be consistent with the second law of thermodynamics. |
| Practically in our realistic universe | Black hole is not black, but it can be actually the brightest objects in our universe because of the radiation of the accretion disk. |
Gravitational Waves
Einstein realized that Newton’s gravity is not consistent with his theory of special relativity. In Newton’s gravity, F = -G M m / r2, the notice of gravitational force should be immediate, even though the distance is very very large. This conflicts with the fact that in the special relativity, there is no rigid body, and nothing could be transmitted super-luminally (faster than light speed).
To solve this contradiction, the equivalence principle probable is a candidate, but it is not very clear how this problem can be solved. So let’s see this problem in another angle. We notice that actually there is a similar problem in electromagnetic field.
Lesson Learned from Electromagnetic Fields
In electromagnetic field, the law in electric field is the Coulomb’s Law F = k Q q / r2 but we also have magnetic field. What actually happens in this situation is, if I move the charge, the whole electric field changes, and it will generate magnetic field which generates electric field again. That is the electric magnetic wave.
In other words, shaking a charge will cause not only the force field changes, but also the electromagnetic wave generated. And the propagation of the electromagnetic wave is consistent with causality, this is consistent with special relativity. The mathematical structure of special relativity, the Lorentz transformation, is actually built in in the theory of electromagnetic field, the Maxwell’s equations.
We can learn a lesson from electromagnetic field: different components, different degrees of freedom in the electric field and magnetic field, they are interchangeably generated and then a wave like behavior is propagated.
Gravitational Waves
And now, what about gravity? General relativity predicts that gravity should have its corresponding waves. You can imagine that excitation degrees of freedom of gravity, which is actually the change of a spherical shape, i.e. deforming the structure of space.
This kind of deformation of space is propagating at the same speed as light speed. The change of space is actually perpendicular to the motion of the wave. In other words, gravitational wave is a transverse wave traveling at the speed of light.
Gravity is an extremely weak force. A small magnet can attract an iron ball, beating the gravity from the whole earth. In order to detect the gravitational wave, we have to look for extremely strong gravitating sources in the universe, say black hole. We had better to have a pair of black holes forming a binary, indeed there are such things in our universe. From the spiral and eventually the merger of the two black holes, we can observe the gravitational waves. And the gravitational waves were first discovered in 2015.
My Certificate
For more on General Relativity: Gravity and Black Holes, please refer to the wonderful course here https://www.coursera.org/learn/understanding-modern-physics-1-relativity-and-cosmology
Related Quick Recap
I am Kesler Zhu, thank you for visiting my website. Check out more course reviews at https://KZHU.ai
Don't forget to sign up newsletter, don't miss any chance to learn.
Or share what you've learned with friends!
Tweet