The first algorithm ever designed for a quantum computer, is the algorithm for solving Deutsch’s problem. The algorithm is an illustration for the mathematical model of quantum computing.
Deutsch’s Problem
Deutsch’s problem is about the function which maps one bit to another bit, i.e. f:{0,1} → {0,1}. There are only 4 types such functions:
- f(x) = 0 (constant)
- f(x) = 1 (constant)
- f(x) = x (balanced)
- f(x) = !x (balanced)
Suppose we are given a function f in a black box, we don’t know which type of the 4 functions seats in the box. The problem is “what function is in the black box?”
In classical case, it appears that we have to query the black box twice, i.e. input 0 and 1 to see what black box returns, to identify the type of the functions. But in quantum case, we could do better.
Recall all quantum operations are performed by unitary operators, and quantum data is represented by vectors in a Hilbert space. Let’s define an operation Uf:
Uf|x⟩|y⟩ → |x⟩|y ⊕ f(x)⟩An interesting property is, when the second qubit is Hadamard |-⟩, the operator Uf won’t change the state, but only the coefficient.
1/√2 Uf|x⟩(|0⟩ - |1⟩)
= 1/√2 (Uf|x⟩|0⟩ - Uf|x⟩|1⟩)
= 1/√2 (|x⟩|0 ⊕ f(x)⟩ - |x⟩|1 ⊕ f(x)⟩)
# if f(x) = 0, |x⟩|0⟩-|x⟩|1⟩ = |x⟩(|0⟩-|1⟩)
# if f(x) = 1, |x⟩|1⟩-|x⟩|0⟩ = -|x⟩(|0⟩-|1⟩)
= 1/√2 (-1)f(x) |x⟩(|0⟩ - |1⟩)
DIY a Quantum Computer
Two of the four functions introduced above use the entangling operator CNOT, which could be implemented using two qubits. We are going to entangle two qubits that are carried by different quantum properties of one photon:
| qubit 1 | position left path: |1⟩right path: |0⟩ |
| qubit 2 | polarization vertical polarization: |1⟩horizontal polarization: |0⟩ |
The main part of the computer is a Mach-Zehnder interferometer, which consists of two semi-transparent mirrors (beam splitters) and two ordinary mirrors (without glass). Note: Mach-Zehnder interferometer is a device very sensitive to the slightest vibration and the slightest deformation of the basement which will change the path length inside the interferometer.
The source of photons could be a simple laser pointer. A polarizer is use to polarize the photo sphere. The functions will be implemented using the two half wave plates (crystals with optical axis). Then we can see the interference picture on the screen, the pattern of the interference will tell us what is inside the interferometer: a constant function, or a balanced function.
Wave Plates
Wave plates are also crystals with optical axis (usually marked as ‘fast’). Photons polarized along this axis pass through this crystal without any trouble (the ordinary beam).
The photons that are polarized orthogonal to this axis also pass through wave plate, but experience a little delay, which actually depends on the thickness of the crystal. We could fit the thickness so the delay will be half wave length. These photons produce the extraordinary beam. When a polarized photon has an angle θ with the ‘fast’ axis, the vertical part of the polarization stays untouched, while the horizontal part is multiplied by -1.
What the wave plates does is exactly the same thing as what the operator Uf does:
1/√2 Uf|x⟩(|0⟩ - |1⟩)
= 1/√2 (-1)f(x) |x⟩(|0⟩ - |1⟩)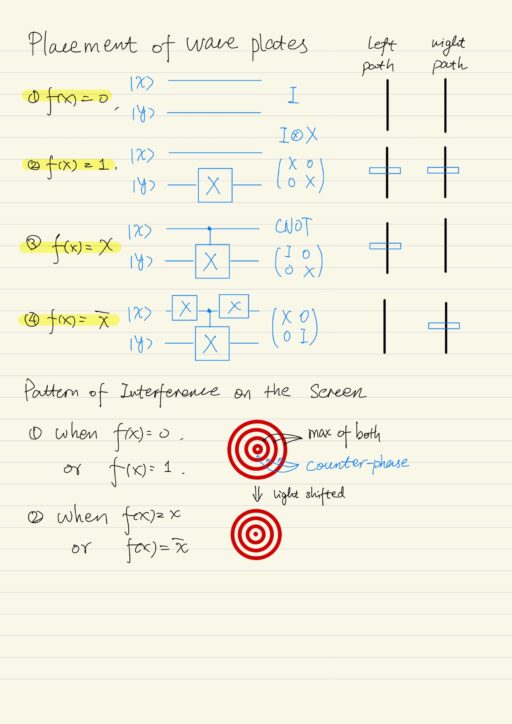
Deutsch-Jozsa Problem
The Deutsch-Jozsa problem is formulated as f: {0,1}n → {0,1}. Similar to the Deutsch problem, this function is either a constant or a balanced, but now there are n qubits map to 1 bit. A balanced function is such a function that returns equal amounts of 1s and 0s.
| x: f(x) = 1 | = | x: f(x) = 0 |Suppose we have a function f resides in a black box. The question is the same as that of the Deutsch problem: Is that function constant or balanced? If you need 100% certainty, then you have to check 2n-1 +1 number of inputs. Again for the quantum case, the thing is much brighter.
We could use almost exactly the same circuits scheme used in the Deutsch problem, except for:
- now we have n qubits
|0⟩nin the first register|x⟩. - we have to apply n-qubit Hadamard transforms.
Only after one application of the operator Uf, we can distinguish balanced function and constant function:
| If it is a constant function | then you always get |0...0⟩ as a measurement result. |
| If it is a balanced function | then you never get |0...0⟩ as a measurement result. |
Bernstein-Vazirani Problem
Bernstein-Vazirani problem is very like the Deutsch-Jozsa problem but with a different definition of f. i.e. a dot product in ℤ2:
f: {0,1}n → {0,1}
f(x) = a ∙ xAgain the function maps n qubits to 1 qubit. We want to know about the number a. Classically, we could feed inputs for n times like |0...010...0⟩ (only one 1 bit in one place) to obtain different bits of a. Quantum computing can solve the problem just with 1 step. The result of the measurement is just |a⟩.
Simon’s Problem
There is a function f mapping from n qubits to n qubits f: {0,1}n → {0,1}n, but with a period a such that f(x) = f(y), i.e. y = x ⊕ a. The problem is to find the period a.
This problem easily becomes intractable, since we need enough memory to store the function values. For example when n = 1000, we need to store 21000 values, which is likely impossible. Even with enough memory, we still need 2n-1 + 1 steps in the worst case to find the inputs for which the function values would be equal. If using quantum computing, we could have a quantum state which holds all the values of the function f in it.
My Certificate
For more on Deutsch’s Problem and DIY a Quantum Computer, please refer to the wonderful course here https://www.coursera.org/learn/quantum-computing-algorithms
Related Quick Recap
I am Kesler Zhu, thank you for visiting my website. Check out more course reviews at https://KZHU.ai
Don't forget to sign up newsletter, don't miss any chance to learn.
Or share what you've learned with friends!
Tweet
