Private Key Encryption - KZHU.ai 🚀

Limitations of Perfect Secrecy

Recall that the perfect secrecy has two limitations:

Key as long as the message
Key can only be used once

The first limitation can be circumvented by relaxing the notion of perfect secrecy to computational secrecy. In particular, the pseudo one time pad scheme allows parties to securely encrypt a very long message using a short key.

In order to circumvent the second limitation, we need to develop an appropriate security definition for the setting where multiple messages can be encrypted using the same key.

In general, security definitions have two parts: security goal and threat model. We will keep the security goal the same and strengthen the thread model.

In fact, we could define a notion of “multiple message secrecy”, instead we define something stronger, namely “security against chosen-plaintext attacks” or CPA-security. Recall that “chosen-plaintext attacks” is one of the thread models, which is defined as:

“In addition to the cipher text whose underlying plain text is unknown, the attacker is able to obtain cipher text encrypted using the same key corresponding to the plain text of the attacker’s choice.”

CPA-security is nowadays the minimum notion of security that an encryption scheme used in practice should satisfy. This thread model is not too strong, and it represents a realistic threat that we need to be concerned about, because in practice, there are many ways an attacker can influence what gets encrypted.

CPA-Security

As usual, we are going to fix an encryption scheme Π, fix a particular adversary A, and define a randomized experiment PrivCPA_A,Π(n), where n is the security parameter:

Obtain a key k ← Gen(1ⁿ).
Allow the attacker, using key k, to submit messages of its choice to an encryption oracle Enc_k(∙), and get back the encryption of the messages.
The attacker outputs a pair of messages m₀ and m₁ of the same length.
We choose a uniform bit b ← {1, 0}.
We encrypt the message c ← Enc_k(m_b) and give c to the attacker.
The attacker can continue to interact with the encryption oracle Enc_k(∙) as many times as it likes.
The attacker A outputs b', A succeeds and the experiment evaluates to 1, if b' = b.

Π is secure against chosen-plainttext attacks (CPA-secure) if for all attackers A, there is a negligible function ε such that:

Pr[ PrivCPA_Π,A(n) = 1 ] ≤ 1/2 + ε(n)

CPA-security is impossible to achieve for deterministic encryption schemes. In order to achieve CPA-security we need to use randomized encryption.

Random (Uniform) Functions

Let Func_n be a set of all functions mapping strings of length n to strings of length n. In general we can represent each function f: {0,1}ⁿ → {0,1}ⁿ by an array of length 2ⁿ, with one entry corresponding to every possible n-bit input, and containing an n-bit value (representing the corresponding output). So we can represent a function using 2ⁿ * n bits, where 2ⁿ is the length of array, n is the length of each element.

This tells us that the size of the set Func_n is exactly equal to the number of strings of length 2ⁿ * n.

|Func_n| = 2^(2ⁿ * n)

A random function is just a member uniformly picked from the set Func_n. In fact, rather than thinking about this being done all at once, we can equivalently think about this being done on-the-fly as values are needed.

Keyed Functions

Keyed functions allow us to define a distribution over functions from n-bit input to n-bit outputs. Let F be a function that takes two inputs and produces one output, i.e. F: {0,1}^* × {0,1}^* → {0,1}^*, assuming F is always efficiently computable in polynomial time in length of both inputs.

Now let’s fix the first input of F as key k, we get F_k(x) = F(k, x). Also assume F is length preserving: |F_k(x)| = |k| = |x|, so for every security parameter n, we have F defined for n-bit keys, n-bit inputs and n-bit outputs. Choosing a uniform k ∈ {0,1}ⁿ is equivalent to choosing the function F_k: {0,1}ⁿ → {0,1}ⁿ. So by choosing a uniform key, we are choosing a function according to some distribution, i.e. F defines a distribution over functions in Func_n.

Pseudorandom Functions (PRFs)

The two-input function F is a pseudorandom function if F_k, for uniform key k ∈ {0,1}ⁿ, is indistinguishable from a uniform function f ∈ Func_n. Formally, for all polynomial time distinguisher D, D can not distinguish between the case when it’s given F_k or when it’s given a completely uniform function f.

| Pr_k←{0,1}ⁿ [D^F_k(∙) = 1] - Pr_f←Funcn [D^f(∙) = 1] | ≤ ε(n)

When D is given
F_k	k is chosen uniformly, number of possible choices is 2ⁿ. D is given access to function F_k to provide input and get output, but D can not look inside the function F_k, and value of k.
f	f is random function, and chosen uniformly from the set of all functions, number of possible choices is 2^(n × 2ⁿ). There is no point for the D to repeat an input because it knows that it’ll get back the same output. The only random here, is the initial choice of f.

F_k is pseudorandom function if D can’t distinguish these possibilities apart.

Pseudorandom functions (PRFs) vs Pseudorandom Number Generators (PRGs)

PRFs are much stronger than PRGs. If we have a PRF, we can easily define various PRGs, for example:

G(k) = F_k(0..0)|F_k(0..1) # maps n-bit seed to 2n-bit output
G(k) = F_k(0)|F_k(1)|F_k(2)|...

PRF can be viewed as a PRG with random access to exponentially long output, and furthermore allows random access to individual chunks of that output.

F_k ⟺ G(k) = F_k(0..0)|...|F_k(1..1)

Pseudorandom Permutations

Let F be a length-preserving keyed function, F is a keyed permutation if:

F_k is a bijection for every k.
F_k^-1 is efficiently computable, where F_k^-1( F_k(x) ) = x.

F is a pseudorandom permutation if F_k, for uniform key k ∈ {0,1}ⁿ, is indistinguishable from a uniform permutation f ∈ Perm_n.

Block Ciphers

Block ciphers are practical constructions of pseudorandom permutations. There is no asymptotics involved. A block cipher is typically defined on some fixed key length n and block length m, and it gives a fixed output length.

F: {0,1}ⁿ × {0,1}^m → {0,1}^m

Because we want this F to be instantiating a pseudorandom permutation, we are going to require that F_k be hard to distinguish from a uniform permutation f ∈ Perm_m. For the case of block cipher, we need to be more stringent.

It is not going to be sufficient for attackers running in polynomial time, we actually want it to be hard even for attackers running in time about 2ⁿ. That is, the best attack should be an exhaustive key search attack.

For large enough n, a random permutation is indistinguishable from a random function; a pseudorandom permutation is similarly indistinguishable from a pseudorandom function. So block ciphers are good pseudorandom functions also. We can use block ciphers both whenever we need pseudorandom permutations as well as we need pseudorandom functions.

AES (Advanced Encryption Standard)

AES (standardized by NIST in 2000) provides a secure instantiation of pseudorandom permutations. AES provides a block length of 128 bits, and 3 different key length: 128, 192, 256 bits. AES with 128-bit keys seems to provide security against attackers running in time 2¹²⁸. There are other block ciphers available, but there is almost no reason to use them.

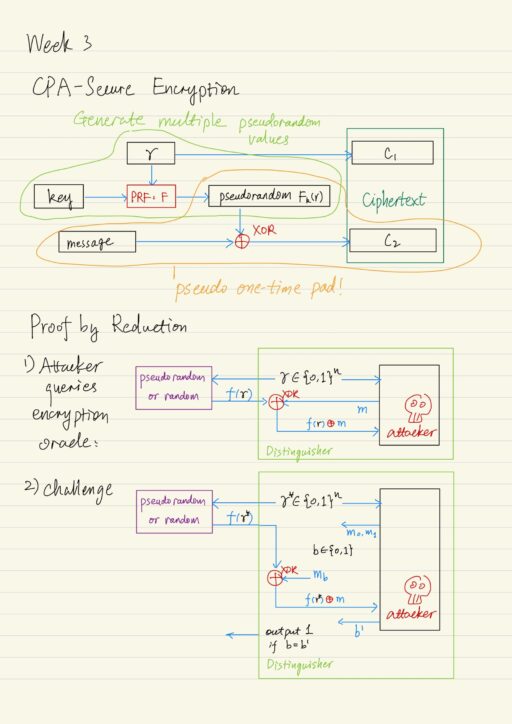
CPA-Secure Encryption

Let F be a keyed function, we define the encryption scheme like this:

Gen(1ⁿ): choose a uniform key k ∈ {0,1}ⁿ, where n is security parameter.
Enc_k(m): randomized encryption of a message m, whose length is same as the key |m| = |k|.
- Choose a uniform r ∈ {0,1}ⁿ.
- Output ciphertext that contains two components: < c₁ = r , c₂ = F_k(r) ⊕ m >.
Dec_k(< c₁, c₂ >): output c₂ ⊕ F_k(c₁) = c2 ⊕ F_k(r).

This scheme integrates the pseudo one time pad, and also has the ability to product multiple independent looking pseudorandom values based on value of r, which was selected uniformly to identify some pseudo randome value in the function table for F_k. This gives us the ability to 2ⁿ different pseudo random values that we can use for encryption. This is why we can use the scheme to safely encrypt more than one message.

Proof by reduction

Prove the theorem: if F is a pseudorandom function, the scheme Π is CPA-secure.

We assume there is an attacker A, attacking our encryption scheme Π. The attacker A is used as a subroutine to construct a distinguisher D, that is trying to distinguish between the two cases:

When it is given a random function.
When it is given access to F_k for a uniform key k.

Since F is a pseudorandom function, then there is no efficient D should be able to tell these apart. Recall in the CPA security experiment, attacker A can access encryption oracle as many times as it wants. So distinguisher D has to provide a way to emulate the encryption oracle.

Attacker A requests encryption of some message m.
D chooses a random uniform value r ∈ {0,1}ⁿ.
D queries the r to the random or pseudorandom functions and get f(r).
D does the XOR operation: m ⊕ f(r).
D provides the attacker A the simulated ciphertext containing both r and m ⊕ f(r).
Repeat this procedure each time A makes a query

At a later moment:

Attacker A outputs 2 messages m0, and m1.
Distinguisher D randomly select 1 message, b ← {0,1}
D encrypts the message m_b as usual, using random value r* and XOR operation.
D provides the attacker A the challenge ciphertext containing r* and m_b ⊕ f(r*).
Attacker can continue to query the encryption oracle as above.
Eventually A outputs a guess b’ as to the message that was actually encrypted.
Distinguisher outputs 1 if b = b’, outputs 0 otherwise.

We now need to analyze two probabilities:

D outputs 1 when it is interacting with a pseudorandom function F_k for a uniform key k.
D outputs 1 when it is interacting with a uniform random function f.

Let μ(n) be the probability that A succeeds in the CPA experiment when interacting with the encryption scheme Π, i.e. μ(n) = Pr[ PrivCPA_A,Π(n) = 1 ]. Let q(n) denote a bound on the total number of encryption queries made by attacker A.

Case 1: When D interacts with a pseudorandom function F_k for a uniform key k:

In this case the view of the attacker A is identical to its view in the CPA experiment. D only outputs 1 exactly when the attacker succeeds. So we have:

Pr_k←{0,1}ⁿ [D^F_k(∙) = 1] = Pr[ PrivCPA_A,Π(n) = 1 ] = μ(n)

Case 2: when D interacts with a uniform random function f:

There are two sub-cases:

r* was queried some other time. The value r* used to construct the challenge cipher was previously used in answering some encryption oracle query. (the event Repeat)
r* was not queried some other time.

Then we can express the probability that D outputs 1 when it is interacting with a uniform random function f:

Pr_f←Funcn [D^f(∙) = 1] ≤ Pr_f←Funcn [D^f(∙) = 1 | ¬Repeat] + Pr[Repeat]

We can bound the probability of repeat: Pr[Repeat] ≤ q(n)/2ⁿ.

If repeat did not occur, then what we know is that the value r* was never queried to the encryption oracle. Because the function f in this case is a uniform function, the value of f(r*) is a uniform n-bit value, independent of the rest of the experiment, the situation is exactly like what we do in one-time pad encryption (with perfect secrecy). So there is no way, whatsoever for the attacker, to determine with probability better than 1/2, i.e. Pr_f←Funcn [D^f(∙) = 1 | ¬Repeat] = 1/2.

Since the F is pseudorandom, we just go through the rest of the math:

| Pr_k←{0,1}ⁿ [D^F_k(∙) = 1] - Pr_f←Funcn [D^f(∙) = 1] | ≤ ε(n)
⟹ |μ(n) - Pr_f←Funcn [D^f(∙) = 1] | ≤ ε(n)
⟹ μ(n) ≤ Pr_f←Funcn [D^f(∙) = 1] + ε(n) ≤ 1/2 + q(n)/2ⁿ + ε(n)

Now the point is for any polynomial q, the term q(n)/2ⁿ is negligible, so finally we get:

μ(n) = Pr[ PrivCPA_A,Π(n) = 1 ] ≤ 1/2 + ε'(n)

This completes the proof, because we showed Π is CPA secure for every polynomial time attacker A, the probability with which that attacker succeeds is bounded by 1/2 plus a negligible function.

Block Cipher: Modes of Operation

With CPA-secure encryption, a 1-block plaintext (of length n) results in a 2-block ciphertext (of length 2n). Encrypting message with arbitrary length is actually easy. Recall that CPA-security implies secrecy for the encryption of multiple messages. So we can encrypt a long message by simply breaking it up into a sequence of n-bit chunks, then applying the encryption scheme to each chunk.

The drawback is that the ciphertext is twice the length of a plaintext. Modes of operations are more efficient mechanisms for encrypting arbitrary-length messages.

Counter mode (CTR mode)

To encrypt a message composed of t blocks, i.e. Enc_k(m₁, …, m_t):

Choose a counter ctr ← {0,1}ⁿ, set c₀ = ctr.
For i = 1 to t: c_i = m_i ⊕ F_k(ctr + i)
Output c₀, c₁, …, c_t.

Ciphertext expansion is just 1 block. It is possible to prove the theorem: if F is a pseudorandom function, the CTR mode is CPA-secure.

Cipher Block Chaining mode (CBC mode)

To encrypt a message composed of t blocks, i.e. Enc_k(m₁, …, m_t):

Choose a random c₀ ← {0,1}ⁿ (also called initialization vector or IV)
For i = 1 to t: c_i = F_k(m_i ⊕ c_i-1)
Output c₀, c₁, …, c_t.

Ciphertext expansion is just 1 block. But the decryption requires F to be invertible (this was not the case for CTR mode). Fortunately block ciphers are invertible so they can be run in the reverse direction. So CBC mode can be decrypted when using a pseudorandom permutation. The theorem is if F is a pseudorandom function, the CTR mode is CPA-secure.

Electronic Code Book mode (ECB mode)

This mode was standardized in 1977, but it is an insecure mode of operation. Don’t use it. The encryption of a message is simply done by applying the pseudorandom function to each message block individually, i.e. Enc_k(m₁, …, m_t) = F_k(m₁), ..., F_k(m_t).

Because this scheme is deterministic, there is no random here, this scheme can not possibly be CPA-secure. In fact it is even worse, because repeated blocks of plaintext can be detected as repeated blocks of cipher text. So ECB mode will not even satisfy our original notion of indistinguishable encryption, that it won’t even be secure for the encryption of a single message.

Attacks from Active Attackers

Malleability

Encryption scheme might be malleable. Informally, if a scheme is malleable if it is possible to modify a ciphertext and thereby cause a predictable change to the plaintext. Malleability can be really dangerous. Perfect secrecy (the strongest notion of security) is not sufficient to imply non-malleability. For example, one-time pad scheme is trivially malleable, the attacker can flip any bit in the ciphertext, and finally flip the corresponding bit in plaintext, and nothing limits the attacker to flipping only a single bit.

Impersonation

Attackers can additionally inject ciphertexts on the communication channel between the send and the receiver. In this setting, we have the attacker as if it were the sender interacting with the receiver, causing the receiver to decrypt injected ciphertexts and give some information back to the attacker. This class of attacks is called chosen-ciphertext attacks.

CCA-Security

Define a randomized experiment PrivCCA_A,Π(n):

Generate key k ← Gen(1ⁿ)
Allow the attacker A(1ⁿ) to interact with both an encryption oracle Enc_k(∙) and a decryption oracle Dec_k(∙).
Attacker A outputs messages m₀, m₁ of the same length.
We choose a message and encrypt it. b ← {0,1}, c ← Enc_k(m_b).
Attacker A can continue to interact with Enc_k(∙) and Dec_k(∙), but may not request decryption of c. (An important restriction results in a meaningful definition that captures any kind of chosen ciphertext attacks that attacker can actually carry out in the real world.)
Attacker A outputs b’; A succeeds if b = b’, and experiment evaluates to 1.

We will say the encryption scheme Π is secure against chosen ciphertext attacks if for all probabilistic polynomial time attackers A, there is a negligible function ε(n), such that:

Pr[ PrivCCA_Π,A(n) = 1 ] ≤ 1/2 + ε(n)

Actually there is a relationship between CCA-Security and the notion of malleability:

If a scheme is malleable, then it can not be CCA-secure.
CCA-security implies non-malleability.

Chosen ciphertext attacks represent a significant, real-world threat. Modern encrytion schemes designed to be CCA-secure.

Arbitrary-Length Messages

In reality, it might not be the case that the length of a message is an integral multiple of the block length of the block cipher. We could encode the original message in some non-cryptographic way, that will allow efficient reconstruction of the original message. Then encrypt the encoded data using encryption to yield the ciphertext.

Message → Encoded data → Ciphertext

One particular encoding scheme is PKCS #5.

PKCS #5

Encoding:

Let L be the block length (in bytes) of the cipher.
Let b be the # of bytes that need to be appended to the message to get length a multiple of L, i.e. 1 ≤ b ≤ L. If the original message length was a multiple of the block length, we actually append additional L bytes of padding to the end of the original message before encrypting it.
Append the value of b (encoded in Hex in 1 byte), b times. For example: if 3 bytes of padding are needed, append 0x030303.

Decoding:

Say the final byte of encoded data has value b.
If b = 0 or b > L, then return error.
If final b bytes of encoded data are not all equal to b, then return error.
Strip off the final b bytes of the encoded data, and output what is left as the message.

Padding oracle

Because receiver could return error, the attacker, by intercepting and modifying ciphertext, can potentially exploit the behavior of the receiver to learn information about a ciphertext. Thus we could call the receiver a padding oracle, who:

takes ciphertext as input,
decrypts them,
checks the encoding,
outputs error when data was incorrectly formatted.

Padding oracles frequently present in web applications. Even if an error is not explicitly returned, an attacker still might be able to detect differences in timing, behavior, etc.

Padding-Oracle Attacks

In practice, the attacker will not be given the full decryption of arbitrary ciphertext. Padding-oracle attack is a real-world example of a chosen ciphertext attack, where only one bit about decrypted ciphertext is leaked to the attacker, but nevertheless, this information can be exploited by an attacker to learn the entire plaintext.

Assume:

The attacker has access to a padding oracle.
CBC mode is used to encrypt and decrypt.
Given two-block ciphertext < IV, c >

The receiver will decrypt the ciphertext, i.e. F_k^-1(c) ⊕ IV to get the encoded data. The attacker does not know the key k, but the main observation is: if an attacker modifies the i-th byte of the IV, this causes a predictable change (only) to the i-th bytes of the encoded data.

F_k^-1(c): ?? ?? ?? ?? ?? ?? ?? ??
                    ⊕
IV:      AB 01 4F 21 00 7C 02 9E
                    =
Encoded: ?? ?? ?? ?? ?? ?? ?? ??

If the attacker modify the first byte of the IV, this will result in a modification only to the first byte of the encoded data.

F_k^-1(c): ?? ?? ?? ?? ?? ?? ?? ??
                    ⊕
IV:      ** 01 4F 21 00 7C 02 9E
                    =
Encoded: $$ ?? ?? ?? ?? ?? ?? ??

Let us assume that in this case there is no error from receiver (successfully decrypted), then the attacker can modify the next byte of the IV and check whether it is successfully decrypted by the receiver. Repeat this process until the receiver returns an error.

F_k^-1(c): ?? ?? ?? ?? ?? ?? ?? ??
                    ⊕
IV:      ** ** ** 21 00 7C 02 9E
                    =
Encoded: $$ ## @@ ?? ?? ?? ?? ??
                ^---- "Error"

This tells the attacker that the exactly final 6 bytes of encoded data are being checked. That in turn means the encoded data were ?? ?? 06 06 06 06 06 06.

Next, the attacker can modify the right-most byte of the IV, in a particular way, to cause a predictable change in the right-most byte of the encoded data. Let us assume the attacker want to change the right-most byte of the encoded data to 07.

F_k^-1(c): ?? ?? ?? ?? ?? ?? ?? ??
                    ⊕
IV:      AB 01 4F 21 00 7C 02 9F
                    =         ^---- 9E to 9F
Encoded: ?? ?? 06 06 06 06 06 07
                              ^---- 06 to 07

So on, modify the final 6 bytes of the IV, until all the final 6 bytes of the encoded data are changed to 07.

F_k^-1(c): ?? ?? ?? ?? ?? ?? ?? ??
                    ⊕
IV:      AB 01 4E 20 01 7D 03 9F
               ^--------------^---- modified
                    =
Encoded: XX XX 07 07 07 07 07 07
               ^--------------^---- 06 to 07

Now attacker can try all possibility for the second byte of the IV, send it to padding oracle to check the response, until it eventually reaches a value for the second byte, at which decryption succeeds.

F_k^-1(c): XX XX XX XX XX XX XX XX
                    ⊕
IV:      AB 41 4E 20 01 7D 03 9F
            ^---- try all possible values 00, 01, ...
                    =
Encoded: XX 07 07 07 07 07 07 07
            ^---- until decryption succeeds!

Now attacker has successfully learned the second byte of the encoded data when the second byte of IV is 41, because XX ⊕ 41 = 07. But in fact the second byte of IV was 01, attacker can determine what XX ⊕ 01 will be equal to:

XX ⊕ 41 = 07
XX ⊕ 01 = (XX ⊕ 41) ⊕ (41 ⊕ 01) = 07 ⊕ 40 = 47

The second byte of the original encoded data transmitted by the sender was equal to 47. At this moment the encoded data is: ?? 47 06 06 06 06 06 06. And the attacker can repeat the process in order to learn the first byte of the encoded data.

Attack Complexity

It takes at most L tries to learn the number of padding bytes. And for each byte of the original plaintext message, it takes at most 2⁸ = 256 tries to cycle through all possibilities. Overall it take # of bytes times 256 for the attacker to learn the entire original message. If the receiver were not doing any sort of throttling to prevent decrypting ciphertext, it would not actually take very long time.

My Certificate

For more on Private Key Encryption, please refer to the wonderful course here https://www.coursera.org/learn/cryptography

My #90 course certificate from Coursera

Related Quick Recap

Computational Secrecy, Pseudo-randomness, and Proof of Security

I am Kesler Zhu, thank you for visiting my website. Check out more course reviews at https://KZHU.ai