Quantum Mechanics: 1-Dimensional Finite Potential Problems

Finite Potential Well

Finite potential well problem is more realistic compared to the infinite potential well. It is specified by this potential profile V(z).

V(z) = 0, -L ≤ z ≤ L
V(z) = V0, otherwise

If the energy of the electron E is greater than the well depth V₀, the electron can escape the potential well and then can free to move around. The case where the energy of the electron is smaller than the depth of the well is called bound state, i.e. 0 < E < V₀. For different region, the Schrödinger equations and solutions are below:

Region I (-L ≤ z ≤ L)	Region II (z ≤ -L) and III (L ≤ z)
(-h2/2m) (d2ψ(z)/dz2) = E ψ(z)	(-h2/2m) (d2ψ(z)/dz2) + V0 ψ(z) = E ψ(z)
ψI(z) = A eikz + B e-ikz	ψII(z) = C ek0z + D e-k0z ψIII(z) = F ek0z + G e-k0z

---

---

Boundary conditions

The potential V is finite everywhere. E < V₀, so E is also finite. Then the second derivative (d²ψ(z)/dz²) in the Schrödinger equation must be finite. Then we have 2 boundary conditions:

1. The first derivative dψ(z)/dz must be finite and continuous.
2. The function ψ itself must be finite and continuous.

The ψ must be finite, which makes D = F = 0 to avoid divergence. The ψ and dψ(z)/dz must be continuous at z = ±L. By applying boundary conditions in two different ways, you will get 2 contradictory conclusions.

tan(kL) = k0 / k       # Symmetric or even parity solution, works when C = G and A = B
cot(kL) = - k0 / k     # Anti-symmetric or odd parity solution, works when C = -G and A = -B

The value of k, k₀ and energy E are determined from the equations here numerically or graphically. You can not solve them analytically. The particles confined inside the well can have only one of the available states.

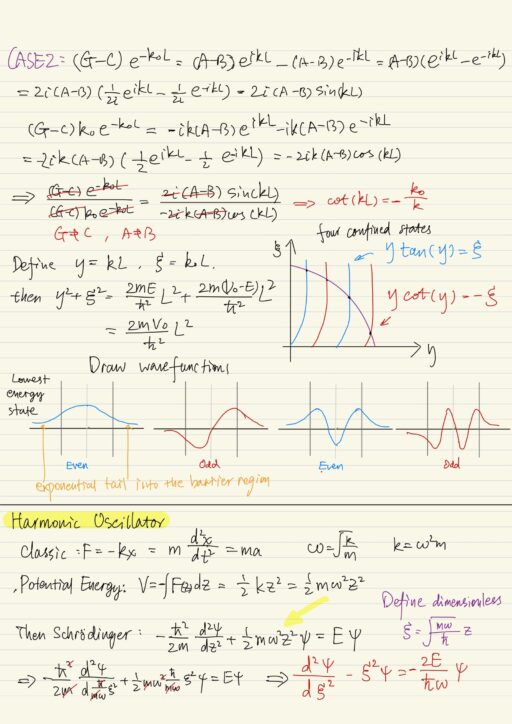
Harmonic Oscillator

The classical harmonic oscillator is a mass m attached to an ideal spring, which exerts a restoring force proportional to the displacement from the equilibrium position. And the constant k here is often called the spring constant.

F = -kz = m d2z/dt2

The solution is a sinusoidal function sin(ωt) with angular frequency ω = √(k/m).

To write down the time-independent Schrodinger equation, we first need to convert the force F into potential energy V because the Schrodinger’s equation is given in terms of potential energy V. Recall the relations between F and V:

V = -∫F(z)dz = (1/2)kz2 = (1/2)mω2z2

Then we have the new Schrödinger equation:

(-h2/2m) (d2ψ(z)/dz2) + (1/2)mω2z2 ψ(z) = E ψ(z)

Define another dimensionless variable ξ = √(mω/h)z , finally the Schrödinger equation becomes:

d2ψ/dξ2 - ξ2ψ = - 2E/hω ψ

We substitute the general solution ψn(ξ) = An Hn(ξ) exp(-ξ2/2) to the Schrödinger equation then we get Hermite Differential Equation. The solutions of the Hermite differential equations are called the hermit polynomial.

All energy levels are all equally spaced by a unit of hω. The energy of the lowest energy state is not 0. Wave functions are Gaussian functions modulated by Hermite polynomial, and all of these functions have a definite parity.

We obtained the solution of harmonic oscillator problem by solving time independent Schrodinger equations. And therefore, there is no time dependence in our solution. It represents a non time varying stationary states, and these stationary solutions do not exhibit any actual oscillation of the classical oscillator.

---

---

Potential Step

The potential step is specified by this potential profile V(z):

V(z) = V0, z > 0
V(z) = 0, z < 0

The particle with an energy E is incident from the left as shown here. E > 0, can be smaller or larger than V₀. Note that E is given to us as part of the initial condition, in this kind of unbound scattering problem. We are not talking about a bound or confined states.

ψI(z) = A eik0z + B e-ik0z
ψII(z) = C eikz + D e-ikz

The solutions actually represents the propagating waves. The initial condition is given that the particle is incident from the left, there should not be any left-propagating wave in region II, so D = 0. We require continuity of wave function ψ and derivative dψ/dz at z = 0, to calculate the constants A, B, and C in solutions.

B and C could be represented by A, but this is a scattering problem and we are interested in obtaining the reflection probability and transmission probabilities. To determine those quantities, we actually don’t have to determine the constant A.

ψI(z) = A [ eik0z + (k0 - k)/(k0 + k) e-ik0z ]
ψII(z) = A 2k0/(k0 + k) eikz

There are 2 major cases we need to consider:

E > V0	Both k and k0 are real and positive. k0 > k. Incident wave: eik0z Reflected wave: e-ik0z Transmitted wave: eikz
E < V0	k0 is real and positive, k is imaginary. Transmitted wave: exponentially decaying There is a non-zero probability of finding the particle inside the barrier region.

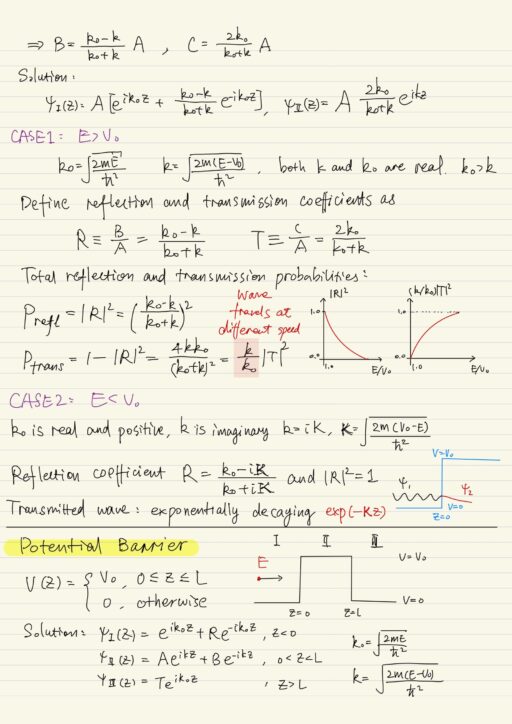
Potential Barrier

The potential step is specified by this potential profile V(z):

V(z) = V0, 0 ≤ z ≤ L
V(z) = 0, otherwise

The particle is incident from the left with an initial energy E, and the energy E is assumed to be greater than zero, it can be either large or greater than the barrier height V₀.

E < V0

Both k and μ are imaginary. There is no propagating wave inside the barrier. Inside the barrier, the wave exponentially decays. Despite that, the barrier has a finite width, and therefore the barrier region ends before the wave function fully decays to zero, which means that there is always a non-zero finite amplitude for the transmitted wave. The transmission probability |T|2 > 0 always: tunneling |T|2 increases monotonically with increasing E. The transmitted wave is evanescent, exponentially decaying inside the barrier region.

E > V0

Both k and μ are real and positive There is always a propagating wave even inside the barrier region. The transmission probability |T|2 interestingly oscillates and reaches unity at particular energy. Apply to negative V0.

---

---

My Certificate

For more on Quantum Mechanics: 1-Dimensional Finite Potential Problems, please refer to the wonderful course here https://www.coursera.org/learn/foundations-quantum-mechanics

My #83 course certificate from Coursera

---

Related Quick Recap

Time-Independent Schrödinger Equation

---

I am Kesler Zhu, thank you for visiting my website. Check out more course reviews at https://KZHU.ai