Shor’s Algorithm

Nowadays, probably Peter Shor’s algorithm for function period finding is the most significant achievement in the field of quantum computing. It allows us to factor big composite numbers in polynomial time.

However for the classical computations, this problem is believed to be hard. For a big number N = p × q, where p and q are two big different primes. In order to find p and q, brute-force search from 2 to √N seems the only classical algorithm that we can perform.

The number p and q can also be seen as secret information hiding in N. There are encryption algorithms based on these asymmetry of multiplication and factoring. The most famous algorithm shall be RSA, which is believed to be secure as long as the factoring problem is believed to be hard. But with Shor’s algorithm, the factoring problem is not hard at all.

---

---

Factoring and the RSA

Private and Public Keys

Suppose p and q are two different primes, and N = p × q. Euler’s totient function φ(N) states the amount of numbers less than N and co-prime to N:

φ(N) = φ(pq) = (p-1)(q-1)

Euler’s theorem also tell us, for any number a co-prime to N, i.e. gcd(a, N) =1, this identity holds:

aφ(N) = 1 (mod N)

We can chose some random number e less than N, and co-prime to both of N and φ(N):

e < N, gcd(e,N) = 1, gcd(e,φ(N)) = 1

Since e is co-prime to φ(N), it is invertible in the ring Z modulo φ(N), i.e. Zφ(N), and its inverse element we called d. We could get this linear representation of the greatest common divisor of φ(N) and e; k and d are coefficients respectively, known as Bézout’s identity.

∃ d < N, e × d = 1 (mod φ(N))
⟹ e × d = 1 + φ(N) × k, or
⟹ e × d + φ(N) × k = 1

Now, public key is defined as (e, N), and private key is defined as (d, N).

Encrypt and Decrypt

To encode message m, the only restriction is m has to be co-prime with N, i.e. gcd(m, N) = 1.

encrypt	c := me (mod N)
decrypt	cd (mod N) = med (mod N) = m(1 + φ(N) × k) (mod N) = m(1) × m(φ(N) × k) (mod N) = m (mod N) = m

The idea is that you can not easily revert the separation of exponentiation modulo N. To revert it, we need the number d. To find d, we need to know φ(N). To know φ(N), we need to know the factors of N, i.e. p and q, which is hard to do if N is really big.

For example:

1. Choose p = 11, q = 13, then N = 143, φ(N) = 10 * 12 = 120.
2. Choose e, which has to be prime to both N and φ(N), say e = 17.
3. Choose message m, which has to be prime to N, say m = 7.
4. Now we have public key (17, 143).
5. Encrypt m to get ciphertext c := 7¹⁷ (mod 143) = 7 * 49⁸ (mod 143) = 7 * 113⁴ (mod 143) = 7 * 42² (mod 143) = 7 * 48 (mod 143) = 50.
6. To get private key 17 * d = 1 + 120 * k. Simply let k = -1, then d will be -7. and in the ring of Z₁₂₀, d = 113.
7. Now we have private key (113, 143).
8. Decrypt c to get message 50¹¹³ (mod 143) = 7.

Factoring and Period Finding

Suppose we have a big composite number N = p × q, where p and q are two different primes. We choose some number a < N, also a is co-prime to N, i.e. gcd(a, N) = 1. If number a appears to be not co-prime to N, then it is easy to derive gcd(a, N) = p or gcd(a, N) = q.

We define function fa(x) = ax (mod N). There must exists a number r, as small as possible, such that ar = 1 (mod N). So any integer smaller than r can’t meet the requirement: ∀ r1 < r ar1 ≠ 1 (mod N). The number r is the period of this function.

ax+r (mod N) = ax × ar (mod N) = ax (mod N)

Assumption 1: the number of r is even, i.e. r = 0 (mod 2).

ar = 1 (mod N)
⟹ ar - 1 = 0 (mod N)
⟹ (ar/2 + 1) (ar/2 - 1) = 0 (mod N)

We can be sure that the second term (ar/2 - 1) can’t be divisible by N. Because if divisible, (ar/2 - 1) = 0 (mod N) will lead to ar/2 = 1 (mod N), which contradicts to our assumption that r is the smallest integer which meets the requirements.

Assumption 2: the first term also can not be divided by N, then we have ar/2 ≠ -1 (mod N).

Based on both assumptions, we have two factors (a^r/2 + 1) and (a^r/2 – 1), their product is divisible by N, but each of the factors is not divisible by N. This means N’s two factors p and q, are situated in (a^r/2 + 1) and (a^r/2 – 1). We can search for it by using Euclidean algorithm.

p, q = gcd(ar/2 ± 1, N)

But the question we must ask is “how much luck do we need for these two assumptions to be true?” The short answer is “it is rather likely”.

---

---

Quantum Fourier Transform

Shor’s algorithm requires the quantum Fourier transform, which is defined as below, where n is the number of qubits.

N := 2n
QFT|x⟩ = 1 / 2n/2 Σ(2^n)-1y=0 e2πixy/N |y⟩

QFT is unitary, it reserves both norm and angles. The matrix of the quantum Fourier transform can be represented by a tensor product of n qubit gates. To implement these gates, we need to use the physical implementation of the phase rotations operator R_k.

The phase rotation operator does not have affect on |0⟩, but will multiplies |1⟩ by the constant e2πi/(2^k).

---

---

Shor’s Algorithm

We have some function f: {0,1}n → {0,1}n, and this function has a period r: ∀x f(x + r) = f(x). We need to search for this period r. This function f would be fa(x) = ax (mod N) with N = 2ⁿ as introduced previously.

The circuit scheme of Shor’s Algorithm is pretty much the same to that of the Simon’s algorithm. The only exception is we have a quantum Fourier transform (in Shor’s) instead of a Hadamard transform (in Simon’s). This is quite reasonable since now we are searching for periods in Z_N (in Shor’s) instead of in Z₂ (in Simon’s).

The measurement after the quantum Fourier transform helps find out the probability of measuring any of the basis vectors |y⟩ of argument state space. The probability is below, where N = 2n, and A ≈ N/r. The number A is the number of times for which the function period r fits into N.

P(y) = 1/AN |ΣA-1j=0 e2πi jry/N|2

Some basis vectors |y⟩ in some sense are better than other. We call them “good |y⟩“. The probability of measuring “good |y⟩“:

P(y) ≥ 4/π2r

There are only r “good |y⟩“, so the probability of measuring any of them is P(y) ≥ 4/π2r × r = 0.406.

Imagine we have this big composite number N, which is the product of two big prime p and q, and we want to factor N. We choose some random number a, we define this function fa(x) and we search for its period r. We employ Shor’s algorithm and some “good |y⟩” with probability almost to 1/2. good y.

Then we search for this k/r in a proximity of 1/N. If we find then we try to use it as a period. If it doesn’t fit we can think that it is one of the denominator. So we have to run Shor’s algorithm many times and to recombine these values that we get. We try to build the value of period. Finally when we succeed, this period may happen to be odd, then we have to start all over.

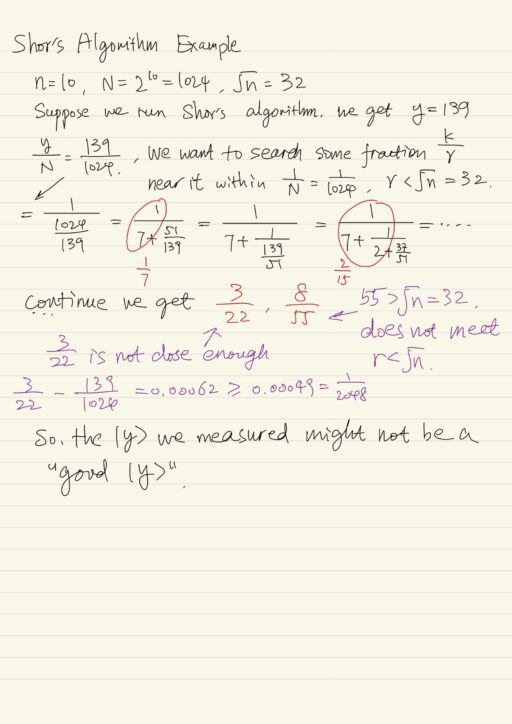
All this seems a little bit time consuming, but it’s not, if compared to the classical approach to this problem. Shor’s algorithm is only O(n2) where n is number of qubits. But all known classical algorithm are over polynomial.

So for big N for classical computing this problem is intractable. But for quantum computation, it’s just a little bit time consuming. Shor’s algorithm provides us with exponential speed up over the classical computing for this task of factoring and period finding.

---

---

My Certificate

For more on Shor’s Algorithm, please refer to the wonderful course here https://www.coursera.org/learn/quantum-computing-algorithms

My #88 course certificate from Coursera

---

Related Quick Recap

Deutsch’s Problem and DIY a Quantum Computer

---

I am Kesler Zhu, thank you for visiting my website. Check out more course reviews at https://KZHU.ai