Physical Basics of Quantum ComputingSaint Petersburg State University It is challenging for lecturers to jam so much knowledge in one course, meanwhile equivalently challenging for learners to grasp the knowledge well. Don’t try this course until you have gotten a solid background in quantum mechanics. I have to admit the first week’s contents cost me…
Tag: Ivan Vybornyi
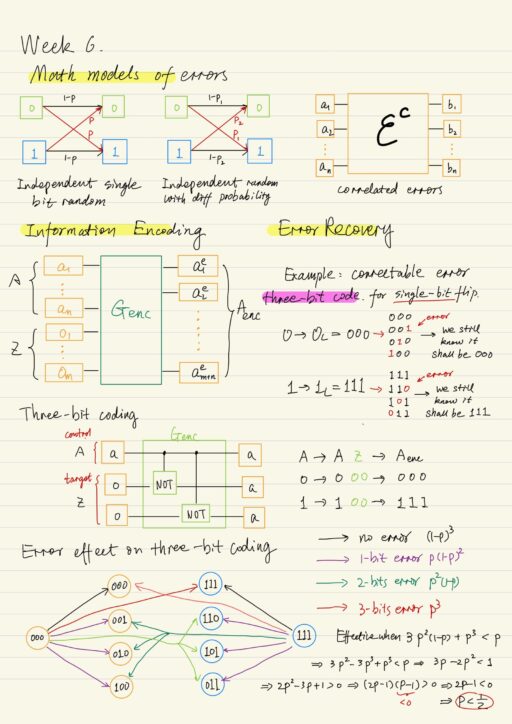
Basics of Quantum Error Correction Theory
The real physical devices that implement computational models are always imperfect. It is not always possible to eliminate all of error sources in practice, however in many cases one could minimize the chances of their occurrence. Classical Error Correction Theory There are three main problems in classical error correction theory: Information channel is an important…
Quantum Algorithms
The essence of the quantum computations might not determine some particular result for a certain function, but establish the global properties of this function. For example, in the Deutsch problem, we don’t find the individual values of a function, but consider the whole superposition of the values and make conclusions about whether the function is…
Transmission of Quantum Information
Unlike the classical bit, as we already know the quantum bit is able to stay in superposition state. When measuring a qubit in superposition state, one obtains every basis state with a certain probability. The probabilistic behavior of quantum objects has its effect on the logical operations. No-cloning Theorem Classical element FANOUT (bit-copying) could be…
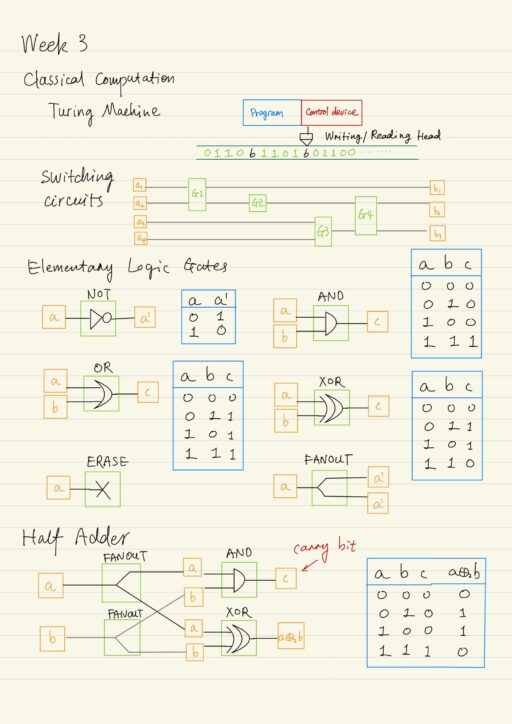
Quantum vs. Classical Logical Operations
Nowadays, there are a large number of various computers. Despite the differences in physical implementations and the purposes of these devices, from the point of view on the computation theory, the operation principle of any of them can be described by Turing “machine”, which is formally called Church-Turing thesis. The main feature and advantage of…
Quantum Entanglement
Quantum entanglement acts as a cornerstone for all quantum computations. If one physical system consists of two or more qubits and its state vector |ζ⟩ can be represented as tensor product |ζ⟩ = |ζ1⟩ ⨂ |ζ2⟩, where |ζ1⟩ and |ζ2⟩ describe states of each qubit. Then the state |ζ⟩ is called separable; otherwise it is…
Statistical Aspects of Quantum Mechanics
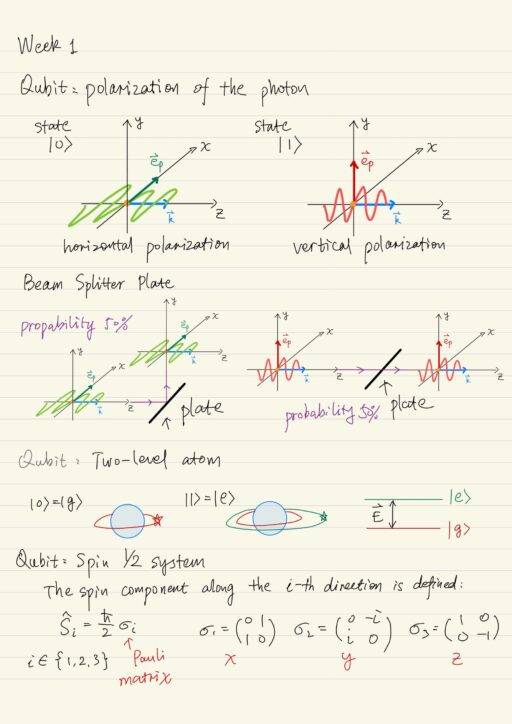
As of now, it is still unclear whether it is possible to create a so-called quantum computer, a special device which will be able to perform a special set of algorithms on the application of quantum mechanical effects. Qubit Implementation A qubit is the smallest element for storing and processing information in a quantum computer….