Into the Unknown
Mathematics for Engineers: The Capstone Course The Hong Kong University of Science and Technology This course is the apex of the entire specialization. It is truly a rewarding journey. I am so excited to learn some basic concepts in computational fluid dynamics (CFD), and to visualize fluid flow around a cylinder with MATLAB. Math is…
Numerical Methods for Engineers The Hong Kong University of Science and Technology This is an excellent course to consolidate your mathematics knowledge with Matlab programming skills. In real life it is usually extremely difficult to find roots, compute quadrature, or solve ordinary differential equations. It is critical to gain the skills to effectively use Matlab….
Vector Calculus for Engineers The Hong Kong University of Science and Technology We can’t emphasize enough the importance of Vector Calculus. A solid understanding lays the foundations for further learning of electromagnetism, fluid mechanics and many disciplines. This course is one of the best I have met. I can’t help but recommend to those who…
Differential Equations for EngineersThe Hong Kong University of Science and Technology By highlighting both theories and applications in practice, this amazing course might be your excellent choice to grasp the differential equations in shortest time. You are actually learning math and physics at the same time, building your own mapping between the 2 disciplines. I…
Gradient Theorem The fundamental theorem of single variable calculus was the one that told you “the integral of the derivative of a function is just going to be the function itself.” The gradient theorem is a generalization of the fundamental theorem of calculus to vector calculus, i.e. calculus of several variables. Suppose a scalar field 蠁, we could use…
Line Integrals Scalar Fields We have a curve C in the x-y plane, we can represent a point on this curve then by a vector r. To do a line integral, we break the curve into small pieces ds, you have a small element of length ds and a value of f on that element, we multiply…
Fourier Series Sometimes complicated motions can actually be composed of motions of many different frequencies. The type of mathematical analysis that’s useful is called Fourier series. Fourier series is a way of representing a function – an infinite series of cosine and sines. You can view these as a linear superposition of waves of various frequencies. We use orthogonality…
Systems of Homogeneous Linear First-order ODEs The system of linear first order homogeneous equations can be written in matrix form. To solve it we’re going to use An ansatz X(t) = V e位t . We’re going to look for solutions of the ansatz. The principle of superposition. When we find solutions of the ansatz, we’ll multiply…
Multidimensional Integration In Vector Calculus, we have to worry about integrating over two or three variables: double integrals or triple integrals. Double integral can be interpreted as a volume, like a single integral is the area under the curve. When the limits don’t depend on any variable, and we could do integrals separately. Polar coordinates Polar coordinates…
Laplace transform Laplace transform is a technique for solving differential equations. By using the Laplace transform you can convert a differential equation into another space where the equation is easier to solve. Laplace transform is a linear transformation and it is invertible. The strength of the Laplace transform technique, is to solve the differential equations where you…
Partial derivatives Partial derivative is to differentiate functions of multiple variables. Assume a function f = f(x, y), you are differentiating f with respect x, that is the usual definition of a derivative of a function of one variable, but y is held constant. There is something called mix partial. It does not depend on…
The general form of inhomogenous linear differential equations is: We need 2 initial conditions x(0) = x0, x'(0) = u0 to have a unique solution, there is a 3-step method to solve it: Solve the homogeneous equation, where g(t) = 0, to find the general solution to the homogeneous equation:xh(t) = C1 x1(t) + C2…
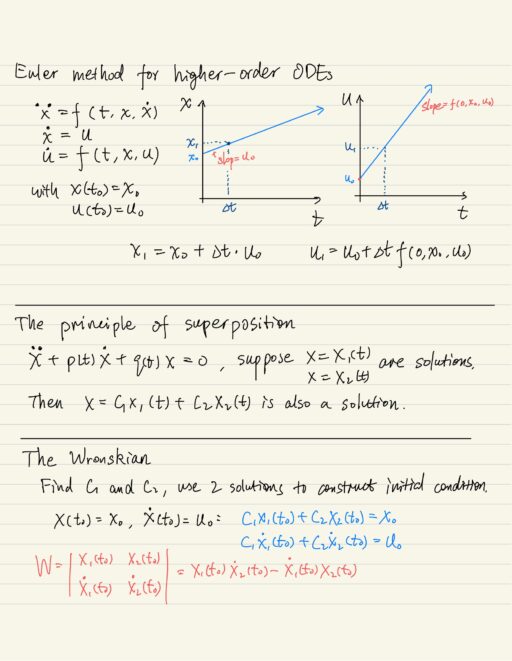
Linear homogeneous differential equation is the second-order ODEs that has the form below, It is important that the function p and q do not depend on x and any of its derivatives: A second-order homogeneous ODE with constant coefficients takes the form below, where a, b and c are constants. Euler Method for Higher-Order ODEs…
Euler Method Euler method is a very simple numerical method that can be used to solve differential equations. For example dy / dx = f(x, y) , there is usually no such a thing as an analytical solution, so one has to solve numerically with an initial condition y(x0) = y0 . Numerical methods approximate…
Vector Calculus is also known as Multivariate Calculus or “Calculus 3”. Calculus 1 and 2 are Differential Calculus and Integral Calculus respectively (both are single variate). Vectors A vector is a quantity that has a length associated with it, and a direction. It is not anchored in any particular spot. Besides, scalars are quantities that…