Multidimensional Integration
In Vector Calculus, we have to worry about integrating over two or three variables: double integrals or triple integrals.
∬A f(x,y) dxdy
∭V f(x, y, z) dxdydzDouble integral can be interpreted as a volume, like a single integral is the area under the curve. When the limits don’t depend on any variable, and we could do integrals separately.
Polar coordinates
Polar coordinates is the most widely used curvilinear coordinate system in two dimensions. Polar coordinates, uses vector r and angle it makes with x-axis θ, instead of x and y. And the length of the vector is denoted by r. We have unit vectors associated with polar coordinates:
- r^ in the direction of increasing r (the length of the vector).
- θ^ in the direction of increasing angle (the angle the vector makes with the x-axis).
They are just a rotation of the i j unit vectors through an angle theta:
r^ = cosθ i + sinθ j
θ^ = -sinθ i + cosθ jThe main difference with these curvilinear coordinate systems with the Cartesian coordinate system, is that the unit vectors depend on the position of the vector (they’re a function of θ). The derivatives of r^ and θ^ with respect to θ have interesting relations.
dr^/dθ = θ^
dθ^/dθ = -r^The del operator ∇ in polar coordinates:
∇ = r^ ∂/∂r + θ^ (1/r) ∂/∂θUsing the operator ∇, we could further define divergence ∇ ∙ u, curl ∇ × u and Laplacian ∇ ∙ ∇ in polar coordinates.
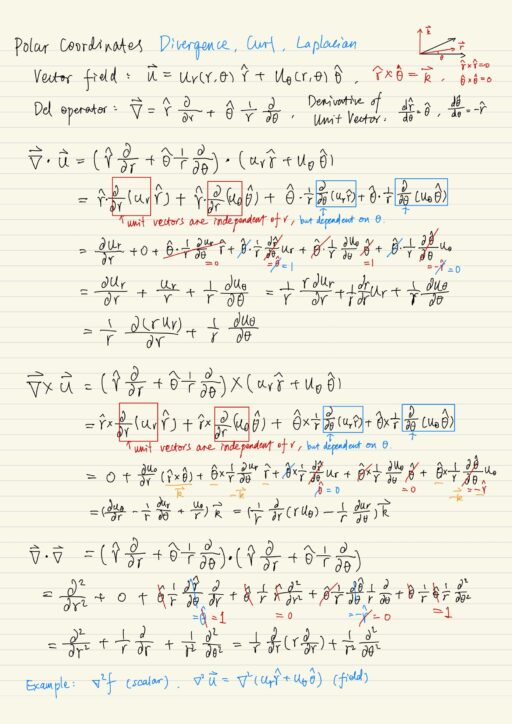
Central force
Newton’s law is F = ma. A central force means that you define your coordinate system so that the force is basically pointing from the object to the origin of the coordinate system.

Change of Variables
It is probable that doing integral is hard in Cartesian coordinates, but easy in Polar coordinates. So to do that, we need to change variables in the integral; from an integral in Cartesian coordinates to an integral in polar coordinates, in 3 steps:
- Substitute the integrand
- Transform the infinitesimal unit, e.g: dxdy
- Change the limits of integration, e.g.: inverse function
When changing variables for double integral, the main difficulty will be transforming infinitesimal unit. It is important to remember the “change of variables formula”:
∬A f(x,y) dxdy
Let x = x(s,t), y = y(s, t)
dxdy = | det(J) | dsdt
J is Jacobian matrix ∂(x, y) / ∂(s, t)
Cylindrical coordinates
Polar coordinates (r, θ) can be extended to 3-dimensional cylindrical coordinates (ρ, φ, z) by adding a new parameter z, which is the vertical height above the x, y plane. The position vector is now wirtten as:
r = ρ ρ^ + z z ^Spherical coordinates
Spherical coordinates (r, θ, ρ) is the geometry associated with a ball or sphere.

My Certificate
For more on Polar, Cylindrical, Spherical Coordinates, please refer to the wonderful course here https://www.coursera.org/learn/vector-calculus-engineers
Related Quick Recap
I am Kesler Zhu, thank you for visiting my website. Check out more course reviews at https://KZHU.ai



