From Partial Derivatives to Maxwell’s Equations

Partial derivatives

Partial derivative is to differentiate functions of multiple variables. Assume a function f = f(x, y), you are differentiating f with respect x, that is the usual definition of a derivative of a function of one variable, but y is held constant. There is something called mix partial. It does not depend on the order that you take derivative. One important use is Taylor series. We can expend functions in terms of their partial derivatives.

Another important application of using partial derivatives is to find minimum of a function, e.g.: minimizing the sum of the squares. We set the partial derivatives with respect to variables to 0. That will give us a system of equations. Then we can solve by any method you like.

---

---

Chain Rule

Total differential tells you how function f is changing when you change both its variables, say x and y.

df = f(x + dx, y + dy) - f(x, y)

Total differential can also be written in partial derivatives.

df = ∂f/∂x dx + ∂f/∂y dy

Suppose, x and y are functions of t, when we got chain rule:0

df/dt = ∂f/∂x dx/dt + ∂f/∂y dy/dt

Triple Product Rule

Assume we have a function f with 3 variables x, y, and z, f(x, y, z) = 0, but they are related x = x(y, z), z = z(x, y):

∂x/∂z ∂z/∂x = 1           # reciprocity relation
∂x/∂y ∂y/∂z ∂z/∂x = -1    # triple product rule

Gradient

The gradient takes the partial derivative and puts them in a vector form. It shows up in all the fundamental equations of nature. The gradient is intrinsically a three dimensional object.

f = f(x, y, z)
df = ∂f/∂x dx + ∂f/∂y dy + ∂f/∂z dz
= (∂f/∂x i + ∂f/∂y j + ∂f/∂z k) ∙ (dx i + dy j + dz k)
= ∇f ∙ dr

df is maximum when ∇f is parallel to dr. If you want to get the maximum change of f, you have to vary your motion in the direction of the gradient. So the direction of the gradient gives you the direction of the maximum change of f, when you move a little bit dr.

Del operator ∇

Differential operator “del” (also called nabla symbol):

∇ = i ∂/∂x + j ∂/∂y + k ∂/∂z

Divergence

Divergence is fundamental to Maxwell’s equations. It means you have a source of something that is going out. We have a vector field:

u = u1(x, y, z) i + u2(x, y, z) j + u3(x, y, z) k

Divergence of u is:

∇ ∙ u = (i ∂/∂x + j ∂/∂y + k ∂/∂z) ∙ (i u1 + j u2 + k u3)
= ∂u1/∂x + ∂u2/∂y + ∂u3/∂z

An important example is the divergence of the electric field from a point charge is zero.

∇ ∙ (r / |r|3) = 0, |r| ≠ 0

Curl

If a vector field has a non-zero curl, it usually means that there’s some swirling motion, some vorticity in the vector field. The curl of a vector field is del cross u, the vector product, which can be calculated using 3 by 3 determinant.

∇ × u = (i ∂/∂x + j ∂/∂y + k ∂/∂z) × (i u1 + j u2 + k u3)
= (∂u3/∂y - ∂u2/∂z) i + (∂u1/∂z - ∂u3/∂x) j + (∂u2/∂x - ∂u1/∂y) k

An important example is the curl of gradient id zero.

∇ × (∇f) = 0

and divergence of a curl is zero:

∇ ∙ (∇ × u) = 0

Laplacian operator ∇²

Laplacian operator is defined as below. It can act on both a scalar field or a vector field. It shows up in a lot of PDEs.

∇2 = ∇ ∙ ∇ = ∂2/∂x2 + ∂2/∂y2 + ∂2/∂z2

Electromagnetic waves

Light waves, radio waves, x-rays are all waves consisting of electric fields E and magnetic fields B. Free space means there is no charges, no currents. Maxwell’s equations in free space can be written:

∇ ∙ E = 0
∇ ∙ B = 0
∇ × E = - ∂B/∂t
∇ × B = μ0ε0 ∂E/∂t

To derive electromagnetic waves, we condense these equations into a single equation for the electric field.

---

---

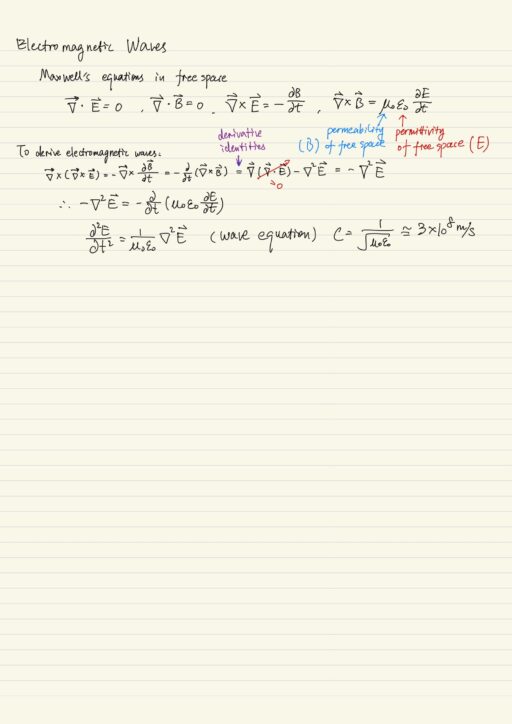
My Certificate

For more on From Partial Derivatives to Maxwell’s Equations, please refer to the wonderful course here https://www.coursera.org/learn/vector-calculus-engineers

My #81 course certificate from Coursera

---

Related Quick Recap

Vector Calculus: Basics

---

I am Kesler Zhu, thank you for visiting my website. Check out more course reviews at https://KZHU.ai