External Motion
Particle in a box is the simplest problem in quantum mechanics. A particle is just translating back and forth between the walls of the box. If there is no external field acting on the particle, i.e. no force acting on the particle except at the walls, then you can decompose the problem into the three coordinate directions x, y, and z, independent of each other.
We’ll solve the x direction, and then the solution will essentially be the same for y and z direction. The box is of length L in the x direction, the motion of the particle is free in the box except at the walls where the potential energy V(r→) goes to a large enough value, say ∞, that the particle cannot penetrate the wall.
V(x) = 0
V(0) = V(L) = ∞The particle can not exist outside the box or at the wall, so the wave function ψ, which is continuous, has to be zero at the wall (boundary conditions):
ψ(0) = ψ(L) = 01-dimensional wave equation for external motion is below, where εx is the x direction translational energy:
(ħ2 / 2m) ∂2ψ/∂x2 = -ψ εx ψThis is just a very simple second order differential equation with sines and cosines as the solution:
ψ(x) = A sin( √(2 m ɛx / ħ2) x ) + B cos( √(2 m ɛx / ħ2) x )To get the coefficient A and B, we have to apply the boundary conditions. We immediately get B = 0 and this, where nx is a positive integer.
ɛx = ħ2 π2 nx2 / (2 m L2)This means is that not all energies are allowed as stationary solutions of the wave equation. That is why the term quantum is used, because only certain quanta of energy are allowed. By applying the postulate which has to do with the normalization, ∫L0|ψ|2dx = 1, we could get A = √(2/L). Finally the solution is below:
ψ(x) = √(2/L) sin( nx π x / L )Increasing nx, it’s easy to imagine that as the quantum number increases, that these solutions become more and more oscillatory to the point where you could hardly tell they were oscillating.
Degeneracy
We could extend the solution above to get total translational energy and wave function in 3 dimensions:
ε = εx + εy + εz = (h2 / 8 m V2/3) (nx2 + ny2 + nz2)
ψ(r→) = √(8/L3) sin( nx π x / L ) sin( ny π y / L ) sin( nz π z / L )This solution leads to an interesting situation: for a given energy ε, there can be more than one solution to the wave equation. This is called degeneracy (denoted as symbol g), in other words, you can have more than one quantum states that contribute to the same energy.
For large values of n, the degeneracy g can be very large. The other consequence of this is basically that translational energy levels are very closely spaced to each other. And as a result, in some instances dealing with translational energy, we’ll be able to treat things in a continuous fashion rather than a quantized fashion.

Internal Motion
Internal motion is about radial and angular motion. It turns out to be convenient to work in spherical coordinates. Again, we pursue separation of variables because we should be able to separate the angular from the radial motion, i.e. ψint(r, θ, ϕ) = R(r) Y(θ, ϕ). We substitute this into the wave equation in spherical coordinates, we end up in separate terms so that the radial terms R are all on the left, and the angular terms Y are on the right. Both sides must equal to a separation constant α.

Angular Motion
We can further separate Y(θ, ϕ) again as Θ(θ)Φ(ϕ), and end up with two equations: one equation is for ϴ, the other one is for Φ, where we’ve chosen β as the separation constant. Totally the angular component of the wave function becomes, where Cl,ml is a normalization constant.
Y(θ, ϕ) = Cl,ml Pl|ml| (cosθ) ei ml ϕIt turns out if we calculate the angular momentum of our system, we would get this below, where l determines the expectation value of the angular momentum and is called angular momentum quantum number.
⟨L2⟩ = l (l + 1) ħ2If we calculate the z component of angular momentum, ⟨Lz⟩ = ml ħ. Normally, atoms or molecules are randomly oriented. However, in the presence of a magnetic field they will align. Thus ml is called the magnetic quantum number.
Then the task is to solve for the radial motion and solve for the angular motion.
Hydrogenic Atom
Hydrogenic means like hydrogen. The hydrogenic atom is just a model atom that has:
- one electron that has a single negative charge, and
- one nucleus that has a single positive charge
the force between the two charges is given by Coulomb’s Law as shown in the equation in the potential energy form V(r) = -e2 / (4 π ε0 r) .

Radial Motion
Recall the particle separation constant α = l (l + 1), and plug α and V into the radial wave equation. To solve the equation, it is usual to transform the equation first to the Laguerre equation. The radial function Rnl is a power series solution, in which the associated Laguerre polynomial L2l+1n+1 is used.
Total Wave Function
Putting radial and angular solutions together, the total wave function is:
ψnlm(r, θ, ϕ) = Rnl(ρ) Yml(θ, ϕ)It is interesting to plot these functions:
- When n=1, l=0, m=0, it is a perfectly spherical solution.
- When n=2, l=0, m=0, it is still a perfectly spherical solution.
- When n=2, l=1, it looks like a “dumbbell”, the value of m decides the orientation of the “dumbbell”.
- When n=3, l=0, m=0, it looks same to n=2, l=0, m=0.
- When n=3, l=1, it looks same to when n=2, l=1.
- When n=3, l=2, you have quite a complicated distribution of electric charge around the nucleus.
All of this, of course, plays a role in how an atom might chemically react with another atom to form a molecule.
Energy Levels
The energy values as a function of the principle quantum number n is given by this relationship, for hydrogen atom, Z = 1:
εn = - Z2 e4 μ / (32 π2 ε02 ħ2 n2), n = 1, 2, 3, ...It’s proportional to one over n, and there’s a minus sign. It is traditional to consider the ionized atom (the atom where the electron is completely removed) as having zero energy. As electrons come in and assumes lower and lower principle quantum numbers, and the energy decreases to the minimum possible value when n equals to 1.
Degeneracy
For this ideal ‘hydrogenic’ atom, the other quantum numbers l and ml, do not affect the energy. However their values are limited by the value of n:
l = 0, 1, 2, ..., n-1
l = i + |ml|, i = 0, 1, 2, ...So the degeneracy for a given principle quantum number n is gn = n2.
Quantum mechanics tells us that electrons, in addition to orbiting the nuclei, have spin. The square of the spinning angular momentum is given by this, where s is the spin angular momentum quantum number, its value is limited to 1/2.
S2 = s (s + 1) ħ2With a general case, there is a z component of the spin, with its own quantum number ms, and that can have values of ±1/2.
Sz = ms ħ
where ms = ±1/2So for our simple hydrogenic atom, the total degeneracy is:
gn = 2n2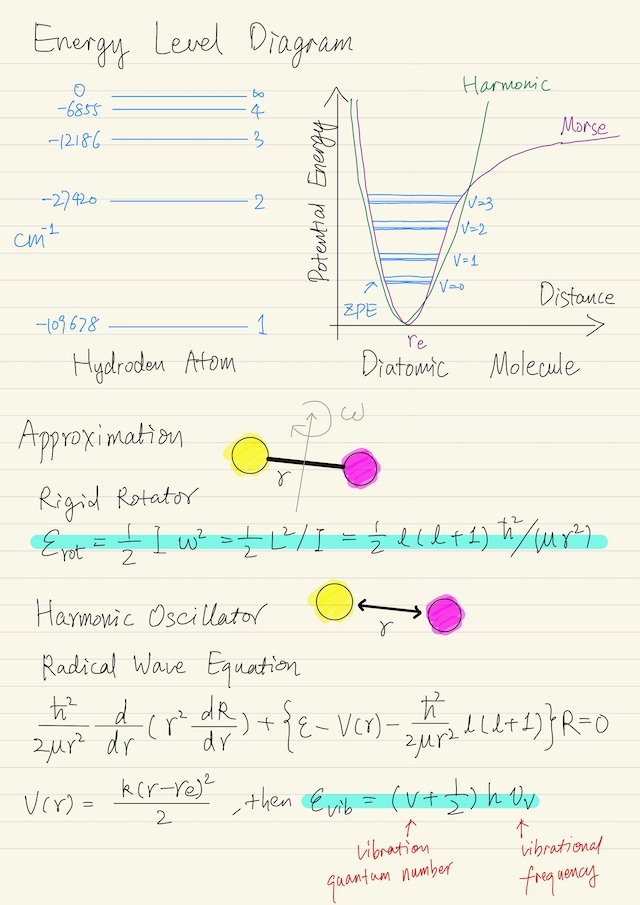
Diatomic Molecule
The most important thing to know about the diatomic molecule is something called the Born-Oppenheimer approximation. This approximation has to do with the fact that electrons are very light compared to nuclei. Electrons move fast, and nuclei move slowly.
For practical purposes, the dynamics of the electrons are in steady-state as the nuclei move. So this was like the quasi-equilibrium approximation in the sense that as we move / rotate / oscillate the nuclei with respect to each other. That those electrons just, pretty instantly on the timescale of the nuclear motions, reach steady-state. That means that we can flip the effect of the electrons as an effective potential force field acting on the nuclei. We can pretend there is a potential force field that gives rise to an effective potential.
If you start with the two nuclei along way apart, there is no force between them. As you bring them together, there is a force it’s called Van der Waals force and it’s a force of attraction. That force will continue until you begin to experience a force of opposition between the positively-charged nuclei, because “likes oppose and opposites attract” in electrostatics.
We’re going to look at analytics solutions for two simple models:
| Rigid rotator | assuming molecule is rigidly bonded (ignoring potential energy) |
| Harmonic oscillator | moderate deviation from the minimum energy position in which the potential energy function looks like a harmonic function. We assume the bond acts like a simple linear spring F = k(r - re), hence potential energy V(r) = k(r - re)2 / 2, where re is the equilibrium value of the radius. |
Rigid Rotator
The angular momentum of any rotating system can be written as its moment of inertia times the rotational frequency, i.e. L = I ω. Moment of inertia for a two mass system is equal to the reduced mass times the separation squared, i.e. I = μ r2. The energy of the system is below, recall L2 = l (l + 1) ħ2.
εrot = 1/2 I ω2
= 1/2 L2 / I
= 1/2 l (l + 1) ħ2 / (μ r2)
= 1/2 J (J + 1) ħ2 / (μ r2)Just for historical purposes, for molecular rotation, it’s common to use J as the rotational quantum number. The degeneracy is gJ = 2J + 1.
Harmonic Oscillator
We’re required to solve the radial wave equation if we want to get numbers for the energy. It turns out that this wave equation can be cast in the form of a Hermite equation and the solution for the energy is below, where v is vibration quantum number, νv (nu_v) is a characteristic vibrational frequency.
εvib = (v + 1/2) h νv
v = 0, 1, 2, ...Note that the energy does not go to zero, and when v = 0, that energy is called the zero-point energy and for vibration, the degeneracy is unity, i.e. gv = 1.
Total Energy
The total rotational and vibrational energy is then:
ε = εrot + εvib
= 1/2 J (J + 1) ħ2 / (μ r2) + (v + 1/2) h νv
where J = 0, 1, 2, ...
v = 0, 1, 2, ...Units
More often, the rotational and vibrational energies expressed in this form, in units of cm-1.
F(J) = εrot / (h c) = Be J (J + 1)
G(v) = εvib / (h c) = ωe (v + 1/2)You can get to inverse centimeters if you divide the energy by Planck’s constant times the speed of light. It was developed by spectroscopists who noted that the inverse of the wavelength of spectroscopic transitions was proportional to the energy difference between the two quantum states involved in the transition.
Alternatively, you can express the energy in terms of characteristic temperatures, which is Kelvin. Be and ωe are in unit cm-1, TR and TV are in units Kelvin.
TR = Be / (k / h c)
TV = ωe / (k / h c)An observation is that Be is much, much less than ωe. That means that the incremental value of rotational energy is much, much less than the incremental value of vibrational energy.
Here is a little unit conversion relationship:
1 e.v.
= 8058 cm-1
= 11600 K
= 1.602e-19 J
= 23.06 kcal/molReal Diatomic Molecules
In a real molecule of course the the rigid rotator, harmonic oscillator approximations are not really valid or exactly valid. Often one can correct for deviation from the simple theory using polynomial expansions in terms of the quantum numbers. The higher order coefficients are typically much smaller than the first order coefficients.
F(J) = Be J (J + 1) - De J2 (J + 1)2 + ...
G(v) = ωe (v + 1/2) - ωe xe (v + 1/2)2 + ωe ye (v + 1/2)3 + ...My Certificate
For more on Hydrogenic Atom and Diatomic Molecule, please refer to the wonderful course here https://www.coursera.org/learn/quantum-mechanics
Related Quick Recap
I am Kesler Zhu, thank you for visiting my website. Check out more course reviews at https://KZHU.ai



