Into the Unknown
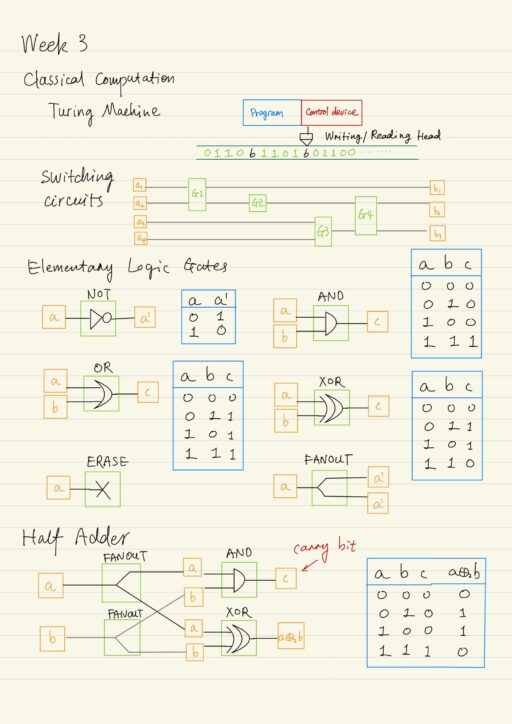
Nowadays, there are a large number of various computers. Despite the differences in physical implementations and the purposes of these devices, from the point of view on the computation theory, the operation principle of any of them can be described by Turing “machine”, which is formally called Church-Turing thesis. The main feature and advantage of…
Quantum entanglement acts as a cornerstone for all quantum computations. If one physical system consists of two or more qubits and its state vector |ζ⟩ can be represented as tensor product |ζ⟩ = |ζ1⟩ ⨂ |ζ2⟩, where |ζ1⟩ and |ζ2⟩ describe states of each qubit. Then the state |ζ⟩ is called separable; otherwise it is…
As of now, it is still unclear whether it is possible to create a so-called quantum computer, a special device which will be able to perform a special set of algorithms on the application of quantum mechanical effects. Qubit Implementation A qubit is the smallest element for storing and processing information in a quantum computer….
Pure and Mixed Ensemble / State In quantum mechanics, we only talk about average or expectation value for a physically observable quantity by taking multiple measurements on ensemble and taking average. Ensemble means a collection of identically prepared physical system. The Stern-Gerlach experiment is an example of producing an ensemble – a collection of electrons…
Time-dependent Schrödinger Equation Time-dependent Schrödinger equations is not an eigenvalue equation, but allowing us to predict the state at t, given the initial condition at t0. where Hamiltonian H^ = -h2/2m ∇2 + V(x, t). The potential energy V(x, t) in general depends on time, however time-independent potential V(x) covers a large number of important…
Commuting Operators Two observables A and B are considered ‘compatible’ if the corresponding operators commute with each other, i.e.: [A^, B^] = 0, where [ ] is commutator bracket, and A^, B^ are operators representing the physical observables A and B. Commuting operators have two very important properties: Commuting operators share the same set of…
Electron Spin Electron has intrinsic angular momentum called spin that is not associated with its orbital motion. And just like orbital angular momentum, spin angular momentum produces magnetic moment. Therefore electrons interact with magnetic field through both orbital and spin angular momentum. The electron is not actually spinning, electron produces angular momentum as if it…
Finite Potential Well Finite potential well problem is more realistic compared to the infinite potential well. It is specified by this potential profile V(z). If the energy of the electron E is greater than the well depth V0, the electron can escape the potential well and then can free to move around. The case where…
Wave-particle Duality The double-slit experiments show us: particle source P1 : probability pattern when slit 1 is openP2 : probability pattern when slit 2 is openP12 = P1 + P2 : probability when both slits are open wave source (intensity of wave I is defined by its amplitude a)I1 = |a1|2 : when slit 1…
Quantum Computing Less Formulas More UnderstandingSaint Petersburg State University My! Oh! My! quantum computing ! This course is stunning! I love the course used plain language to make complicated quantum mechanics topics easy to understand. To me, the quantum teleportation and cryptography topics are profoundly amazing. I am like Alice going down the rabbit hole. Strongly recommend! My Certificate I am Kesler Zhu, thank you…