First of all, a quick introduction to 4 the most important figures in thermodynamics: Sadi Carnot (1796-1832) who discovered the second law of thermodynamics. Rudolf Clausius (1822-1888) who restated the Sadi Carnot’s principle into the form we use today. William Thomson (Lord Kelvin, 1824-1907) who brought thermodynamics into its modern form. Max Planck (1858-1947) who…
Category: Physics
My #84 course certificate from Coursera
Physical Basics of Quantum ComputingSaint Petersburg State University It is challenging for lecturers to jam so much knowledge in one course, meanwhile equivalently challenging for learners to grasp the knowledge well. Don’t try this course until you have gotten a solid background in quantum mechanics. I have to admit the first week’s contents cost me…
Thermodynamics: Fundamental Concepts
Thermodynamics is the study of the equilibrium behavior of systems, for which motion at the microscopic level of atom and molecules is important. It involves solving problems that arise because of work, heat transfer, mass transfer interactions with a working substance of some kind. Microscopic behavior determines macroscopic properties such as PVT relations, internal energy…
My #83 course certificate from Coursera
Foundations of Quantum MechanicsUniversity of Colorado Boulder This is a challenging course. If you are serious about learning quantum mechanics, I highly recommend this course to you. Furthermore if you want to engage yourself with quantum computing, this course is an excellent choice to lay the foundations. Your quest starts here: the time-independent Schrödinger equation…
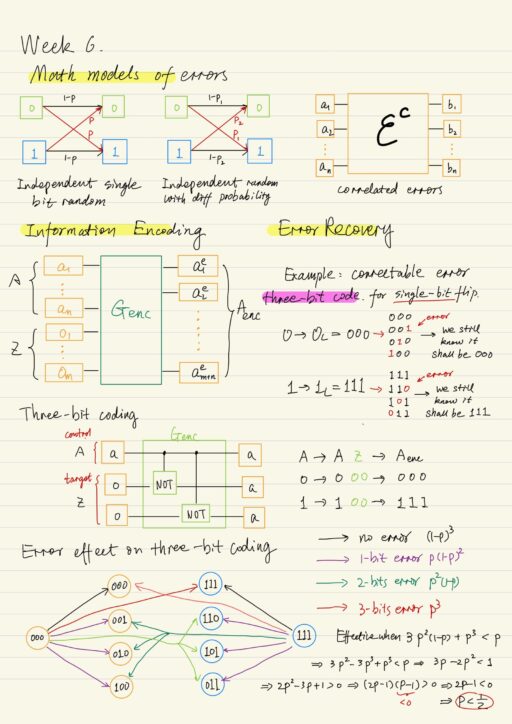
Basics of Quantum Error Correction Theory
The real physical devices that implement computational models are always imperfect. It is not always possible to eliminate all of error sources in practice, however in many cases one could minimize the chances of their occurrence. Classical Error Correction Theory There are three main problems in classical error correction theory: Information channel is an important…
Quantum Algorithms
The essence of the quantum computations might not determine some particular result for a certain function, but establish the global properties of this function. For example, in the Deutsch problem, we don’t find the individual values of a function, but consider the whole superposition of the values and make conclusions about whether the function is…
Transmission of Quantum Information
Unlike the classical bit, as we already know the quantum bit is able to stay in superposition state. When measuring a qubit in superposition state, one obtains every basis state with a certain probability. The probabilistic behavior of quantum objects has its effect on the logical operations. No-cloning Theorem Classical element FANOUT (bit-copying) could be…
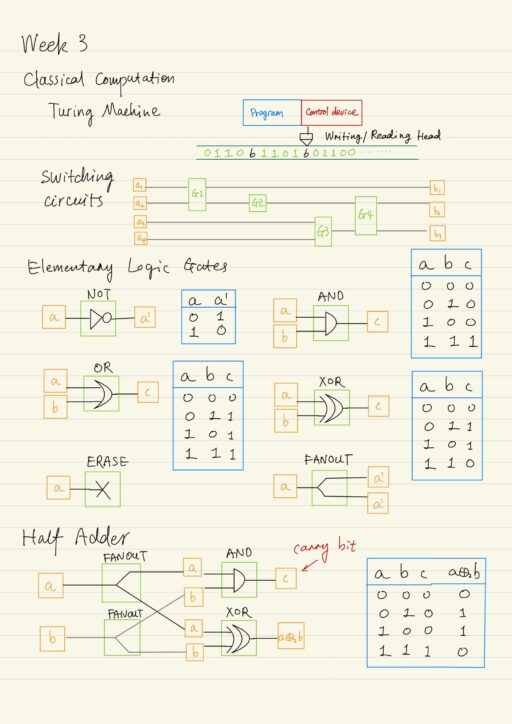
Quantum vs. Classical Logical Operations
Nowadays, there are a large number of various computers. Despite the differences in physical implementations and the purposes of these devices, from the point of view on the computation theory, the operation principle of any of them can be described by Turing “machine”, which is formally called Church-Turing thesis. The main feature and advantage of…
Quantum Entanglement
Quantum entanglement acts as a cornerstone for all quantum computations. If one physical system consists of two or more qubits and its state vector |ζ⟩ can be represented as tensor product |ζ⟩ = |ζ1⟩ ⨂ |ζ2⟩, where |ζ1⟩ and |ζ2⟩ describe states of each qubit. Then the state |ζ⟩ is called separable; otherwise it is…
Statistical Aspects of Quantum Mechanics
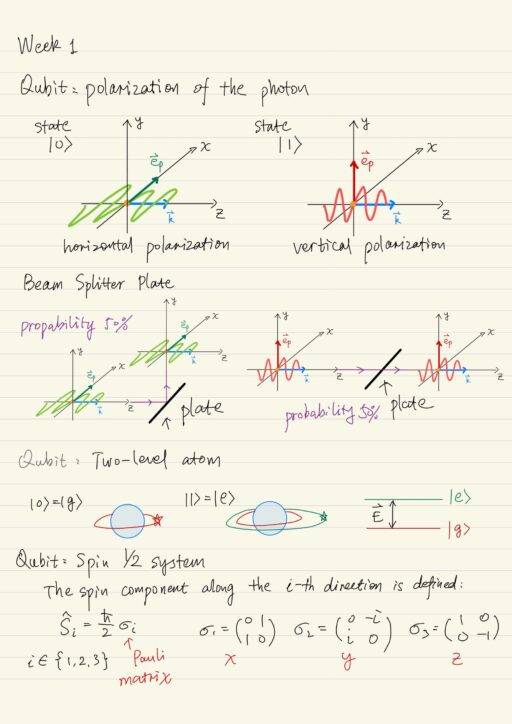
As of now, it is still unclear whether it is possible to create a so-called quantum computer, a special device which will be able to perform a special set of algorithms on the application of quantum mechanical effects. Qubit Implementation A qubit is the smallest element for storing and processing information in a quantum computer….
Quantum Mechanics: Ensembles and Identical Particles
Pure and Mixed Ensemble / State In quantum mechanics, we only talk about average or expectation value for a physically observable quantity by taking multiple measurements on ensemble and taking average. Ensemble means a collection of identically prepared physical system. The Stern-Gerlach experiment is an example of producing an ensemble – a collection of electrons…
Time Evolution of Quantum States
Time-dependent Schrödinger Equation Time-dependent Schrödinger equations is not an eigenvalue equation, but allowing us to predict the state at t, given the initial condition at t0. where Hamiltonian H^ = -h2/2m ∇2 + V(x, t). The potential energy V(x, t) in general depends on time, however time-independent potential V(x) covers a large number of important…
Quantum Mechanics: Uncertainty Principle and Change of Basis
Commuting Operators Two observables A and B are considered ‘compatible’ if the corresponding operators commute with each other, i.e.: [A^, B^] = 0, where [ ] is commutator bracket, and A^, B^ are operators representing the physical observables A and B. Commuting operators have two very important properties: Commuting operators share the same set of…
Stern-Gerlach Experiments & Dirac Bra-ket Notation
Electron Spin Electron has intrinsic angular momentum called spin that is not associated with its orbital motion. And just like orbital angular momentum, spin angular momentum produces magnetic moment. Therefore electrons interact with magnetic field through both orbital and spin angular momentum. The electron is not actually spinning, electron produces angular momentum as if it…
Special Relativity: Space and Time
For hundreds years, space and time were absolute in the concept of Newton, they are something that can not be changed. Since a hundred years ago, we understood special relativity, space and time were put together – one object that can transform to each other. Further, we have general relativity that space and time are not…